Classification non supervisée - Clustering
Méthodes de partitionnement et algorithme k-Means
Roland Donat
BUT Science des Données
Objectifs de la séance
- Rappeler la problématique de partitionnement des données
- Présenter la méthode des centres mobiles (k-Means)
Généralités

Rappels
Qu'est ce qu'une classification non supervisée
- C'est rechercher des regroupements "naturels" entre des individus
- Le nombre de groupes n'est pas connu a priori
- Aucune connaissance sur les classes des individus n'est disponible a priori
- Il s'agit d'une méthode de statistique exploratoire permettant de comprendre les données
Objectifs de la classification non supervisée
- Construire des groupes homogènes et interprétables vis-à-vis de l'objectif recherché
- Les individus au sein d'un groupe doivent être aussi semblables que possible au sens d'un ou plusieurs critères donnés
- Les individus de groupes distincts doivent être aussi différents que possible au sens des mêmes critères
Qu'est qu'une partition
Partition d'un ensemble d'individus
- Soit \(\boldsymbol{X}\) un tableau de données contenant \(N\) individus \(\{\boldsymbol{x}_{1}, \ldots, \boldsymbol{x}_{N}\}\).
- Les ensembles d'indices \(C_{1}, \ldots, C_{k}, \ldots, C_{K} \subseteq \{1, 2, \ldots, N\}\)
forment une partition, notée \(C\), des données \(\boldsymbol{X}\) en \(K\) classes
si :
- Pour tout \(k\), \(C_{k} \neq \varnothing\), i.e. aucune classe n'est vide
- \(\bigcup_{k=1}^{K} C_{k} = \{1, \ldots, N \}\), i.e. la réunion des classes contient les indidces de tous les individus du jeu de données \(\boldsymbol{X}\)
- Pour tout \(k_{1}, k_{2}\), \(C_{k_{1}} \cap C_{k_{2}} = \varnothing\) si \(k_{1} \neq k_{2}\), i.e. les classes sont deux à deux disjointes
Exemples
- Considérons un jeu de données à 5 individus \(\boldsymbol{X} = \{\boldsymbol{x}_{1}, \boldsymbol{x}_{2}, \boldsymbol{x}_{3}, \boldsymbol{x}_{4}, \boldsymbol{x}_{5}\}\)
- L'ensemble \(C_{1} = \{1, 2, 3, 4, 5\}\) est une partition à une classe, i.e. \(K = 1\)
- Les ensembles \(C_{1} = \{1, 3, 5\}\) et \(C_{2} = \{2, 4\}\) forment une partition à deux classes, i.e. \(K = 2\)
- Les ensembles \(C_{1} = \{4, 5\}\), \(C_{2} = \{1\}\), \(C_{3} = \{3\}\) et \(C_{4} = \{2\}\) forment une partition à quatre classes, i.e. \(K = 4\)
Résumé statistique d'une partition
Résumé statistique d'une classe
- Soit \(\boldsymbol{X}\) un tableau de données contenant \(N\) individus \(\{\boldsymbol{x}_{1}, \ldots, \boldsymbol{x}_{N}\}\) définis dans \(\mathbb{R}^{D}\)
- Considérons une partition à \(K\) classes, notée \(C = \{C_{1},\ldots,C_{K}\}\)
- Chaque classe \(C_{k}\) peut, entre autres, être caractérisée par :
- son effectif : \(N_{k} = \text{Card}(C_{k})\)
- son centre (point moyen, centre de gravité) : \[ \boldsymbol{\mu}_{k} = \frac{1}{N_{k}}\sum_{n \in C_{k}} \boldsymbol{x}_{n} = \left(\frac{1}{N_{k}}\sum_{n \in C_{k}} x_{n, 1}, \ldots, \frac{1}{N_{k}}\sum_{n \in C_{k}} x_{n, D}\right) \]
- la dispersion autour de son centre caractérisée par la matrice de variance-covariance empirique de la classe : \[ \boldsymbol{W}_{k} = \frac{1}{N_{k} - 1}\sum_{n \in C_{k}} (\boldsymbol{x}_{n} - \boldsymbol{\mu}_{k})(\boldsymbol{x}_{n} - \boldsymbol{\mu}_{k})^{T} \]
- son inertie de classe (cas équipondéré) : \(I_{\boldsymbol{\mu}_{k}}(C_{k}) = \sum_{n \in C_{k}} d(\boldsymbol{x}_{n}, \boldsymbol{\mu}_{k})^{2}\)
Résumé statistique d'une partition
Exemple (1/2)
| exports | health | income | cls | |
|---|---|---|---|---|
| country | ||||
| Samoa | 29.20 | 6.47 | 5400 | c3 |
| Iraq | 39.40 | 8.41 | 12700 | c3 |
| Netherlands | 72.00 | 11.90 | 45500 | c1 |
| Paraguay | 55.10 | 5.87 | 7290 | c3 |
| Oman | 65.70 | 2.77 | 45300 | c1 |
| Suriname | 52.50 | 7.01 | 14200 | c3 |
| Mauritius | 51.20 | 6.00 | 15900 | c3 |
| Central African Republic | 11.80 | 3.98 | 888 | c2 |
| Rwanda | 12.00 | 10.50 | 1350 | c2 |
| Afghanistan | 10.00 | 7.58 | 1610 | c2 |
| Switzerland | 64.00 | 11.50 | 55500 | c1 |
| Mauritania | 50.70 | 4.41 | 3320 | c2 |
| Ireland | 103.00 | 9.19 | 45700 | c1 |
| Congo, Rep. | 85.10 | 2.46 | 5190 | c3 |
| Chad | 36.80 | 4.53 | 1930 | c2 |
| Ecuador | 27.90 | 8.06 | 9350 | c3 |
| Guinea-Bissau | 14.90 | 8.50 | 1390 | c2 |
| Thailand | 66.50 | 3.88 | 13500 | c3 |
| Mongolia | 46.70 | 5.44 | 7710 | c3 |
| Lao | 35.40 | 4.47 | 3980 | c2 |
- Effectifs dans chaque classe :
| cls | c1 | c2 | c3 |
|---|---|---|---|
| Effectif | 4 | 7 | 9 |
- Centres de gravité des classes :
| exports | health | income | |
|---|---|---|---|
| cls | |||
| c1 | 76.17 | 8.84 | 48000.00 |
| c2 | 24.51 | 6.28 | 2066.86 |
| c3 | 50.40 | 5.96 | 10137.78 |
- Matrices de variances des classes :
| exports | health | income | ||
|---|---|---|---|---|
| cls | ||||
| c1 | exports | 331.66 | 9.27 | -38096.67 |
| health | 9.27 | 17.80 | 9294.67 | |
| income | -38096.67 | 9294.67 | 25026666.67 | |
| c2 | exports | 262.75 | -25.66 | 14842.79 |
| health | -25.66 | 6.59 | -1329.49 | |
| income | 14842.79 | -1329.49 | 1303275.81 | |
| c3 | exports | 322.60 | -29.53 | -2354.50 |
| health | -29.53 | 3.58 | 2318.15 | |
| income | -2354.50 | 2318.15 | 16140744.44 |
Résumé statistique d'une partition
Exemple (2/2)
Formalisation du problème de partitionnement
Un problème complexe...
Nombre de partitions possibles
- Dans la suite, nous noterons \(\mathcal{C}_{K}(\boldsymbol{X})\) l'ensemble de toutes les partitions possibles de \(\boldsymbol{X}\) en \(K\) classes
- Le nombre de partitions à \(K\) classes possibles pour un jeu de données \(\boldsymbol{X}\) contenant \(N\) individus est donnée par \[ S(N, K) = \frac{1}{K!} \sum_{j=0}^{K} (-1)^{K-j} \binom{K}{j} j^{N} = \text{Card}(\mathcal{C}_{K}(\boldsymbol{X})) \]
- L'ordre de grandeur est donc \(\text{Card}(\mathcal{C}_{K}(\boldsymbol{X})) \simeq \frac{K^{N}}{K!}\)
- Pour \(N=19\) et \(K=4\), il existe plus de \(10^{10}\) possibilités !
Formalisation du problème de partitionnement
Qualité d'une partition
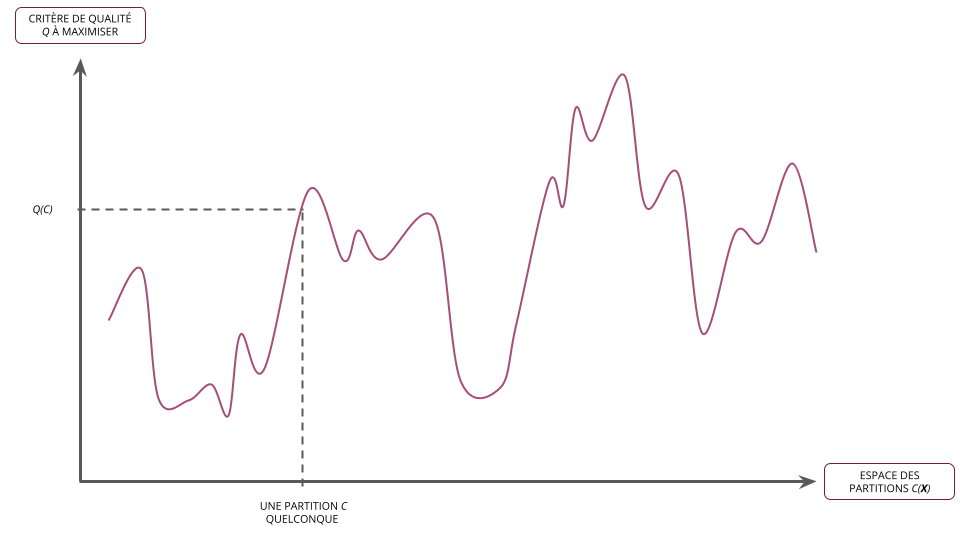
Critère de qualité d'une partition
- Soit \(\boldsymbol{X}\) un ensemble d'individus
- On définit un critère de qualité sur une partition \(C = \{C_{1}, \ldots, C_{K}\} \in \mathcal{C}_{K}(\boldsymbol{X})\) comme étant une fonction de la forme : \[ Q : \mathcal{C}_{K}(\boldsymbol{X}) \rightarrow \mathbb{R}^{+} \]
- Plusieurs critères de qualité \(Q\) peuvent être définis mais tous partagent en général le point commun de mesurer l'homogénéité des classes
- Rappel : \(\mathcal{C}_{K}(\boldsymbol{X})\) est l'ensemble de toutes les partitions possibles de \(\boldsymbol{X}\) en \(K\) classes
Exemples de critère de qualité
- Inertie intra-classe : \(Q(C) = \sum_{k=1}^{K} \sum_{i \in C_{k}} d(\boldsymbol{x}_{i}, \boldsymbol{\mu}_{k})^{2}\) (cas équipondéré)
- Vraisemblance des individus au sein de chaque classe compte tenu du modèle de partitionnement choisi (critère probabiliste)
Formalisation du problème de partitionnement
Problème d'optimisation
Le partitionnement comme problème d'optimisation
- Soit \(\boldsymbol{X}\) un ensemble d'individus
- Soit \(Q\) un critère de qualité de partitionnement en \(K\) classes
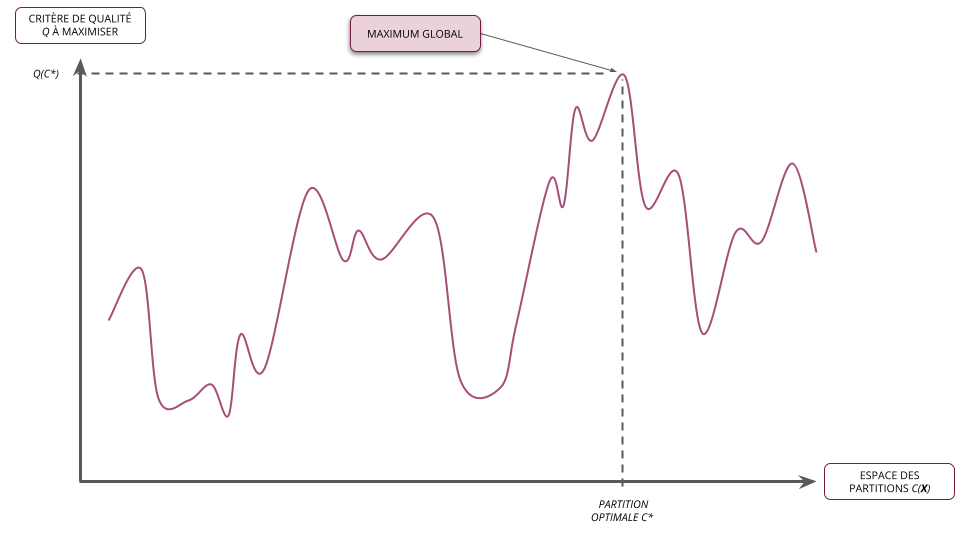
- Résoudre le problème de partitionnement des données \(\boldsymbol{X}\) en \(K\) classes revient à trouver la partition optimale \(C^{*} \in \mathcal{C}_{K}(\boldsymbol{X})\) qui maximise le critère de qualité \(Q\)
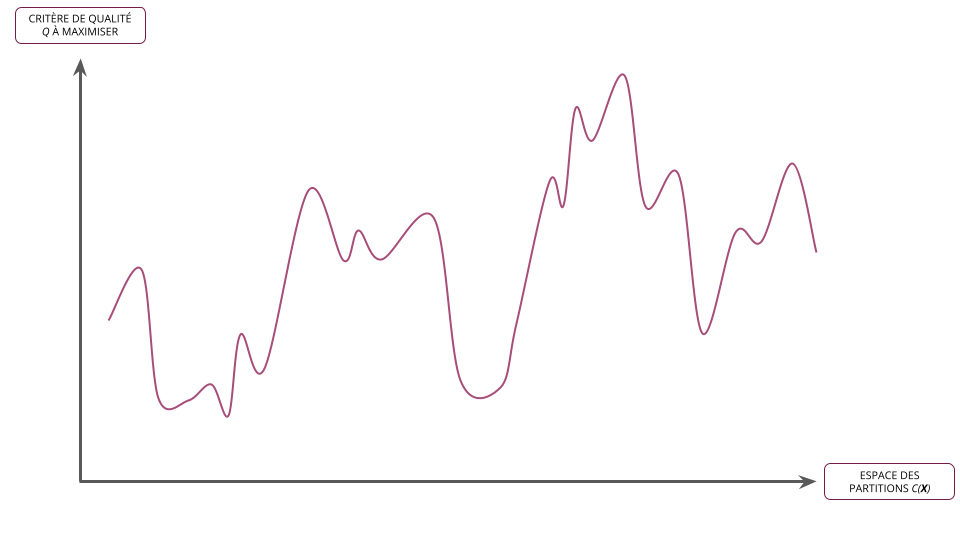
- Il s'agit donc d'un problème d'optimisation classique que l'on peut écrire formellement : \[ C^{*}_{K} = \arg\max_{C \in \mathcal{C}_{K}(\boldsymbol{X})} Q(C) \]
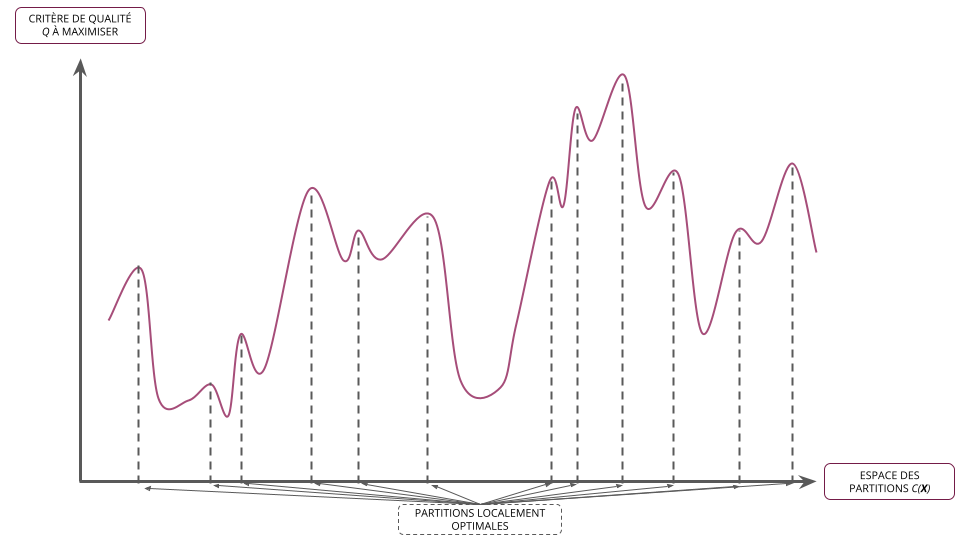
Problème combinatoire
- La formulation du problème d'optimisation relatif au partitionnement d'individus est simple
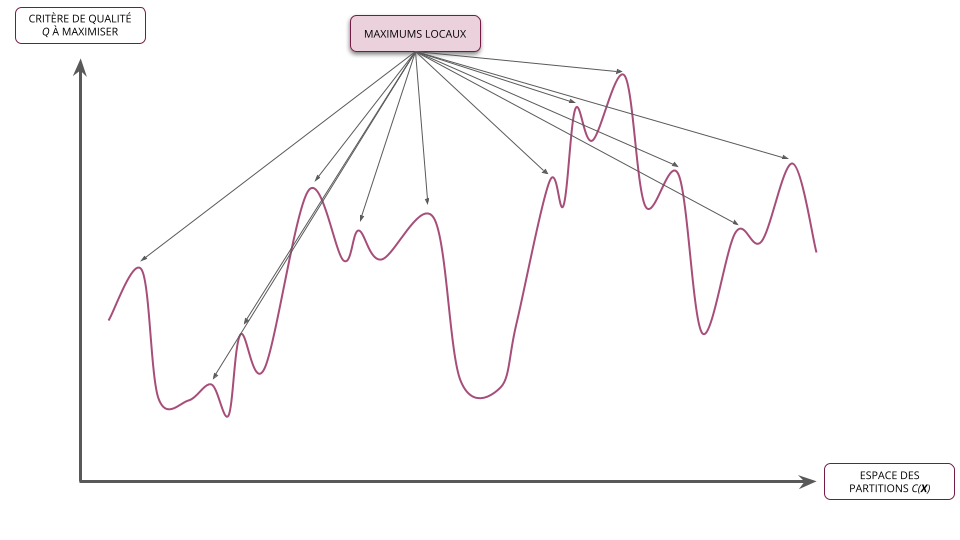
- Sa résolution exacte est toutefois inenvisageable en pratique de par la combinatoire des solutions à explorer
- Les méthodes de partitionnement ne cherchent donc pas à trouver la meilleur partition au sens du critère choisi (i.e. l'optimum global) mais plutôt à limiter l'exploration des partitions tout en assurant de trouver une "bonne" partition pour ce critère (i.e. un optimum local)
Formalisation du problème de partitionnement
Problème d'optimisation
Formalisation du problème de partitionnement
Problème d'optimisation
Formalisation du problème de partitionnement
Problème d'optimisation
Formalisation du problème de partitionnement
Problème d'optimisation
Formalisation du problème de partitionnement
Problème d'optimisation
Formalisation du problème de partitionnement
Résolution itérative
Principe général des algorithmes de partitionnement
- Soit \(\boldsymbol{X}\) un ensemble d'individus
- Soit \(Q\) un critère de qualité de partitionnement en \(K\) classes
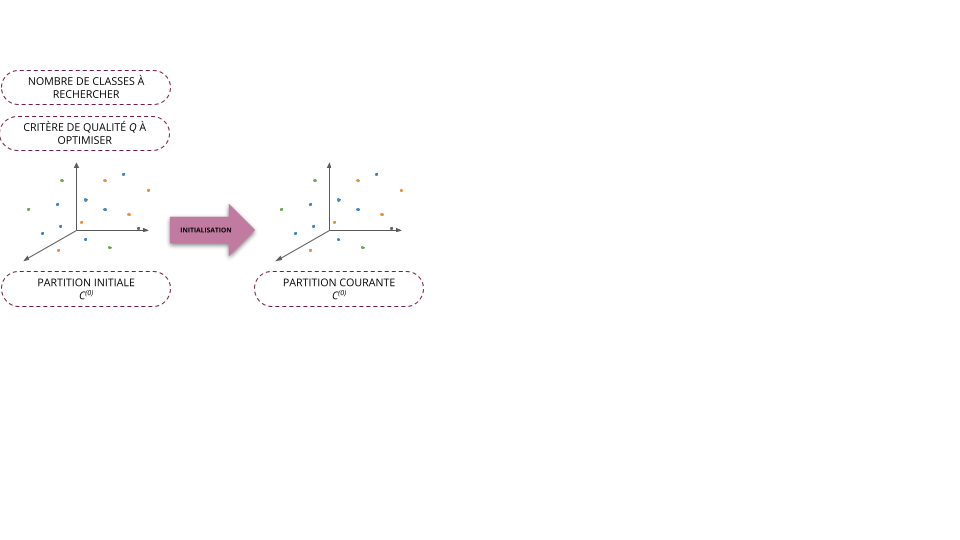
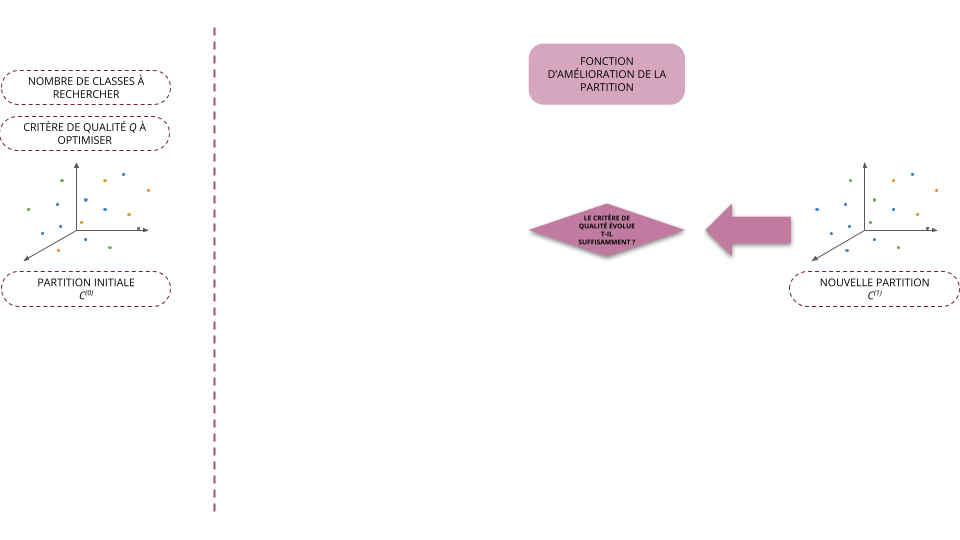
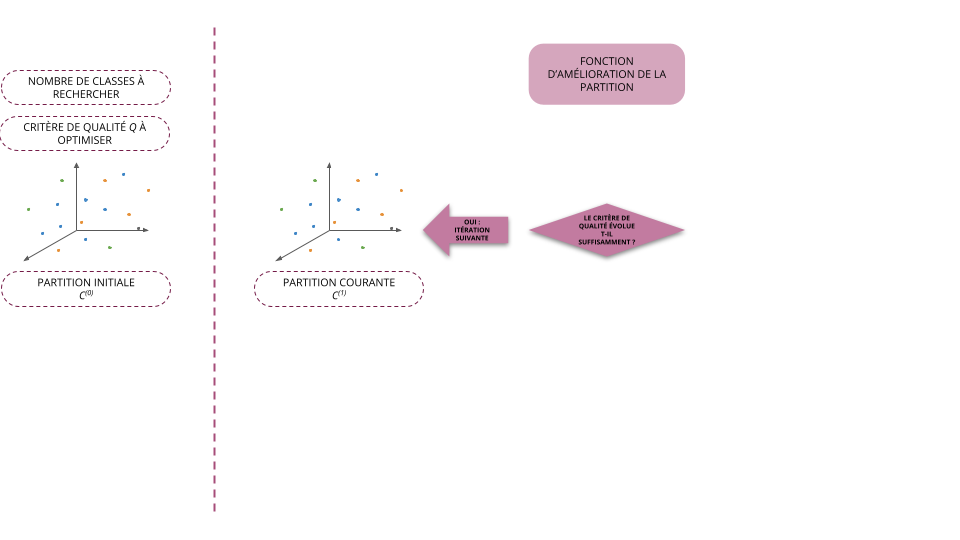
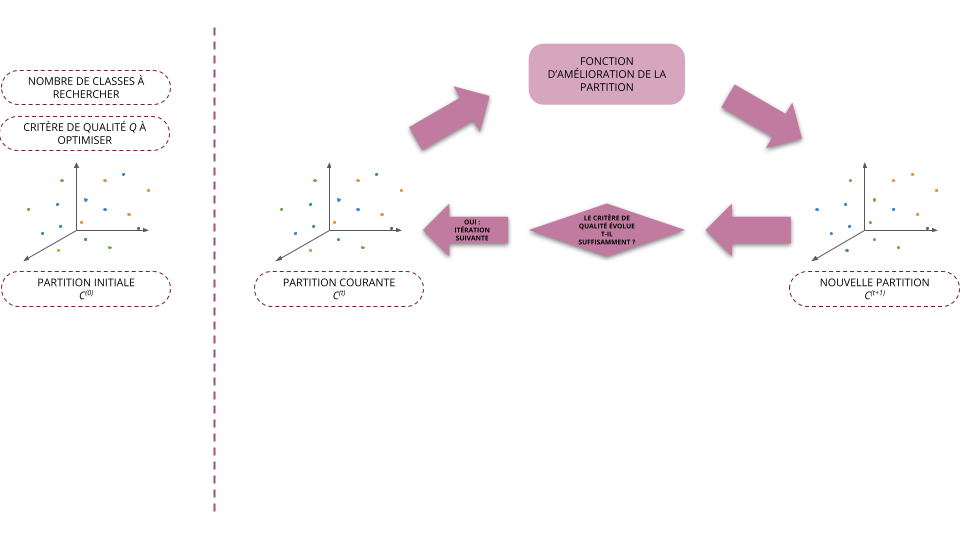
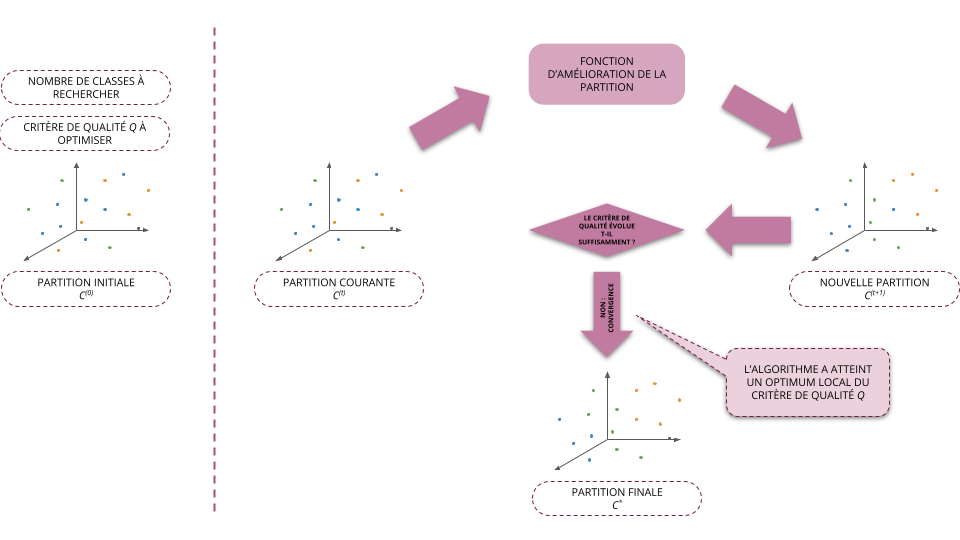
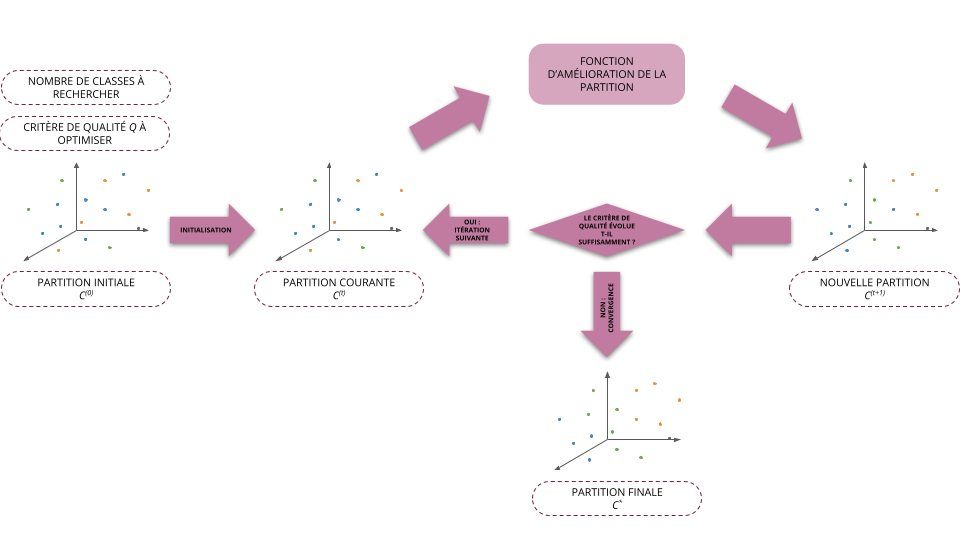
- Les algorithmes de partitionnement reposent sur le schéma itératif général suivant :
- Initialisation (\(t=0\)): on part d'une partition initiale \(C^{(0)}\) (choisi arbitrairement)
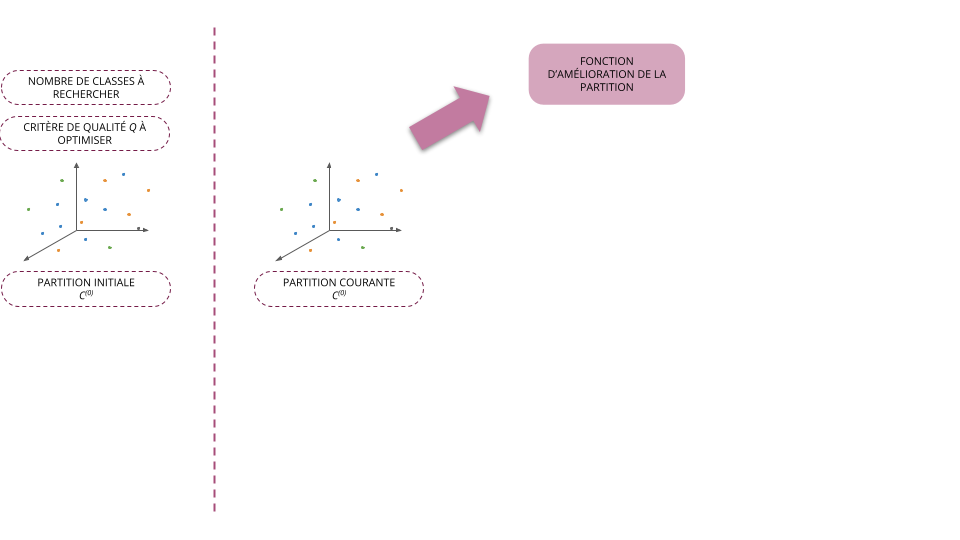
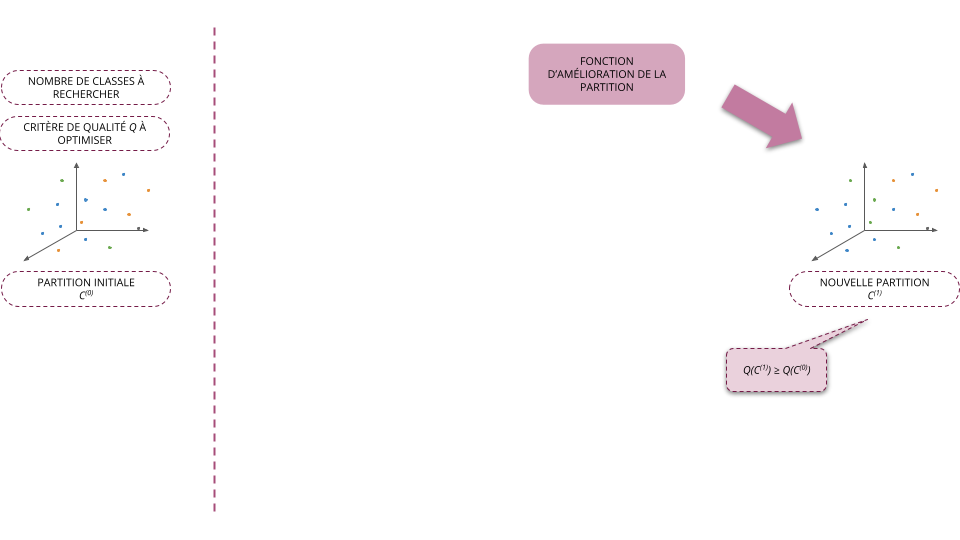
- À l'étape \(t + 1\), on cherche la partition \(C^{(t+1)} = f(C^{(t)})\) telle que \(Q(C^{(t+1)}) \ge Q(C^{(t)})\)
- On arrête l'algorithme dès que le critère de qualité a convergé, i.e. qu'il ne varie plus suffisamment d'une itération à l'autre
- La plupart des méthodes utilisées aujourd'hui reposent sur ce schéma et ne diffèrent donc qu'au niveau de la fonction \(f\) permettant d'améliorer la classification des individus à partir d'une partition donnée
Formalisation du problème de partitionnement
Résolution itérative

Formalisation du problème de partitionnement
Résolution itérative
Formalisation du problème de partitionnement
Résolution itérative
Formalisation du problème de partitionnement
Résolution itérative
Formalisation du problème de partitionnement
Résolution itérative
Formalisation du problème de partitionnement
Résolution itérative
Formalisation du problème de partitionnement
Résolution itérative
Formalisation du problème de partitionnement
Résolution itérative
Formalisation du problème de partitionnement
Résolution itérative
Méthode des moyennes mobiles (k-Means)

Principe général
Principe de la méthode
- Objectif : on cherche à partitionner un ensemble d'individus \(\boldsymbol{X}\) dans \(\mathbb{R}^{D}\) en \(K\) classes \(C_{1}, \dots, C_{K}\)
- Procédure :
- Initialisation : On commence par affecter (arbitrairement ou aléatoirement) une classe à chaque individu
- Étape de calcul des centres : On calcule les centres des classes \(\boldsymbol{\mu}_{1}, \ldots, \boldsymbol{\mu}_{K}\) sur la base de la partition de \(\boldsymbol{X}\) courante
- Étape d'affectation des classes : On met à jour la classe de chaque individu \(\boldsymbol{x}_{n}\) en choisissant celle dont le centre est le plus proche au sens d'une distance donnée (par exemple la distance euclidienne)
- Critère d'arrêt de la procédure : On retourne à l'étape de calcul des centres tant que la partition change d'une itération à l'autre
Principe général
Exemple
Caractéristiques
Paramètres de la méthode
La méthode des centres mobiles nécessite de choisir :
- Le nombre de classes \(K\) à construire
- Une première partition des individus pour initialiser la méthode
- Une distance pour évaluer la proximité entre les individus et le centre des classes
Point de vigilance 1
- Le partition construite par la méthode dépend des deux éléments suivants :
- La partition initiale choisie
- La distance utilisée
- En fonction de ces deux choix, la méthode n'aboutira pas forcément aux mêmes résultats
Point de vigilance 2
- En grande dimension (i.e. quand il y a beaucoup de variables), la distance euclidienne entre les individus tend à grandir et à perdre son caractère discriminant
- Autrement dit, tous les individus se retrouvent très éloignés les uns des autres
- Réduire au préalable le nombre de dimensions (e.g. par ACP) peut donc s'avérer pertinent dans ce cas
Caractéristiques
Exemple - influence de l'initialisation
Caractéristiques
Exemple - influence de la distance
Algorithme des centres mobiles
Entrée : \(\boldsymbol{X} = \{\boldsymbol{x}_{1}, \ldots, \boldsymbol{x}_{N}\}\) un ensemble d'individus dans \(\mathbb{R}^{D}\)
Paramètres :
- \(K\) : Nombre de classe à construire
- \(C^{(0)} = \{C^{(0)}_{1}, \ldots, C^{(0)}_{K}\}\) : Une première partition des individus
- \(d\) : Une distance définie sur \(\mathbb{R}^{D}\)
Sortie : Une partition \(C^{*} = \{C^{*}_{1}, \ldots, C^{*}_{K}\}\) des individus
Itération \((t)\) :
- Calcul des centres des classes : \(\displaystyle \boldsymbol{\mu}^{(t)}_{k} = \frac{1}{\left|C^{(t-1)}_{k}\right|} \sum_{i \in C^{(t-1)}_{k}} \boldsymbol{x}_{i}, ~\forall k = 1, \ldots, K\)
- Affectation de la classe de chaque individu \(n \in \{1, \ldots, N\}\) : \[ \left\{ \begin{array}{l} k^{*} = \arg\min_{k \in {1, \ldots, K}} d(\boldsymbol{x}_{n}, \boldsymbol{\mu}^{(t)}_{k}) \\ C^{(t)}_{k^{*}} \leftarrow C^{(t)}_{k^{*}} \cup \{n\} \end{array} \right. \]
Critère d'arrêt : Plusieurs choix possibles
Algorithme des centres mobiles
Remarques
Plusieurs critères d'arrêt possibles
- Si l'algorithme dépasse un nombre d'itérations limite \(T\), i.e. si \(t > T\)
- Si la partition n'évolue plus d'une itération à l'autre, i.e. si pour tout \(k \in \{1, \ldots, K\}\), \(C^{(t)}_{k} = C^{(t-1)}_{k}\)
- Si l'inertie intra-classe descend sous un certain seuil \(\epsilon\), i.e. si \(I_{\text{W}}(C^{(t)}) < \epsilon\)
- Si l'inertie intra-classe ne décroît pas suffisamment entre deux itérations, i.e. si \(I_{\text{W}}(C^{(t)}) - I_{\text{W}}(C^{(t-1)}) < \epsilon\)
Convergence de l'algorithme et complexité
- La méthode des centres mobiles converge vers une partition qui optimise localement l'inertie intra-classe
- La méthode ne trouve donc pas forcément la meilleur partition, i.e. celle qui minimise globalement l'inertie intra-classe
- La vitesse de convergence de l'algorithme est de l'ordre \(\mathcal{O}(T K N D)\), \(T\) étant le nombre maximal d'itérations autorisé
- Il s'agit donc d'un algorithme de complexité polynomial - donc plutôt rapide
Algorithme des centres mobiles
Exemple : Déroulé de la méthode
Algorithme des centres mobiles
Exemple : Déroulé de la méthode
Données
| life_expec | total_fer | |
|---|---|---|
| country | ||
| Afghanistan | 56.20 | 5.82 |
| Antigua and Barbuda | 76.80 | 2.13 |
| Armenia | 73.30 | 1.69 |
| Benin | 61.80 | 5.36 |
| Bhutan | 72.10 | 2.38 |
| Botswana | 57.10 | 2.88 |
| Cape Verde | 72.50 | 2.67 |
| Colombia | 76.40 | 2.01 |
| Cyprus | 79.90 | 1.42 |
| Denmark | 79.50 | 1.87 |
| Guatemala | 71.30 | 3.38 |
| Iraq | 67.20 | 4.56 |
| Ireland | 80.40 | 2.05 |
| Jamaica | 74.70 | 2.17 |
| Macedonia, FYR | 74.00 | 1.47 |
| Moldova | 69.70 | 1.27 |
| Mozambique | 54.50 | 5.56 |
| Poland | 76.30 | 1.41 |
| Qatar | 79.50 | 2.07 |
| Uzbekistan | 68.80 | 2.34 |
Évolution au cours des itérations
Partition
| iter_cur | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| country | |||||
| Afghanistan | c2 | c2 | c2 | c2 | c2 |
| Antigua and Barbuda | c2 | c0 | c0 | c0 | c0 |
| Armenia | c2 | c0 | c1 | c1 | c1 |
| Benin | c2 | c2 | c2 | c2 | c2 |
| Bhutan | c0 | c0 | c1 | c1 | c1 |
| Botswana | c2 | c2 | c2 | c2 | c2 |
| Cape Verde | c0 | c0 | c1 | c1 | c1 |
| Colombia | c1 | c0 | c0 | c0 | c0 |
| Cyprus | c1 | c0 | c0 | c0 | c0 |
| Denmark | c2 | c0 | c0 | c0 | c0 |
| Guatemala | c0 | c1 | c1 | c1 | c1 |
| Iraq | c2 | c2 | c1 | c1 | c1 |
| Ireland | c0 | c0 | c0 | c0 | c0 |
| Jamaica | c1 | c0 | c0 | c0 | c0 |
| Macedonia, FYR | c2 | c0 | c0 | c1 | c1 |
| Moldova | c1 | c2 | c1 | c1 | c1 |
| Mozambique | c1 | c2 | c2 | c2 | c2 |
| Poland | c2 | c0 | c0 | c0 | c0 |
| Qatar | c2 | c0 | c0 | c0 | c0 |
| Uzbekistan | c0 | c2 | c1 | c1 | c1 |
Position du centre de classes
| life_expec | total_fer | |||||
|---|---|---|---|---|---|---|
| cls | c0 | c1 | c2 | c0 | c1 | c2 |
| iter_cur | ||||||
| 0 | 73.02 | 71.04 | 70.17 | 2.56 | 2.49 | 2.93 |
| 1 | 76.28 | 71.30 | 62.19 | 1.95 | 3.38 | 3.97 |
| 2 | 77.50 | 70.70 | 57.40 | 1.84 | 2.61 | 4.90 |
| 3 | 77.94 | 71.11 | 57.40 | 1.89 | 2.47 | 4.90 |
| 4 | 77.94 | 71.11 | 57.40 | 1.89 | 2.47 | 4.90 |
Inertie intra-classe et % d'inertie expliquée
| IW | PctI | |
|---|---|---|
| iter_cur | ||
| 0 | 1236.12 | 2.2% |
| 1 | 366.76 | 71.0% |
| 2 | 117.44 | 90.7% |
| 3 | 114.17 | 91.0% |
| 4 | 114.17 | 91.0% |
Avantages/Limitations de la méthode
Avantages
- Méthode facile à comprendre et à implémenter
- Algorithme rapide et adapté au traitement d'un grand nombre de données
- Convergence vers une partition localement optimale
Limitations
- l'algorithme recherche des classes de forme sphérique et de même taille
- Difficulté à fonctionner en grande dimension (Comme toutes les méthodes reposant sur une distance)
- Convergence vers une partition localement optimale
Choix du nombre de classes
Rappel
- Plus on augmente le nombre de classes et plus l'inertie intra-classe diminue
- Nous avons même \(I_{\text{W}} = 0\), si le nombre de classes \(K\) est identique au nombre d'individus \(N\)
Stratégies possibles
- Expertise : Vous avez une idée plus ou moins précise sur le nombre de groupes à former
- Tests automatiques : On réalise différents partitionnements en faisant varier le nombre de
classes et on utilise un critère pour sélectionner la valeur optimale, e.g. :
- Méthode du "coude", approche visuelle
- Critère AIC (Akaïke Information Criterion) ou BIC (Bayesian Information Criterion), approche plus formelle nécessitant une reformulation du problème de classification automatique dans le cadre probabiliste
- Stabilité des partitions, on retient le nombre de classes qui permet d'obtenir les partitions les plus stables malgré une initialisation aléatoire
Choix du nombre de classes
Exemple : méthode du "coude"
Résumé de la séance
Points clés
- Le problème de partition des données est un problème combinatoire extrêmement complexe
- Les algorithmes de partitionnement usuels ne cherchent pas à construire la partition optimale mais plutôt une bonne partition
- La méthode des moyennes mobiles est une méthode de partitionnement géométrique simple à mettre en oeuvre permettant de classer les individus dans des groupes ayant des caractérisques homogènes
Merci pour votre attention !
Des questions ?
