Classification non supervisée - Clustering
Classification hiérarchique
Roland Donat
BUT Science des Données
Objectifs de la séance
- Définition du concept de hiérarchie
- Définir la notion de distance entre classes
- Comprendre l'algorithme de classification ascendante hiérarchique (CAH)
- Savoir interpréter un dendrogramme
Généralités
Rappels et objectifs
Qu'est ce qu'une classification non supervisée
- C'est rechercher des regroupements "naturels" entre des individus
- Le nombre de groupes n'est pas connu a priori
- Aucune connaissance sur les individus n'est disponible a priori
- Il s'agit d'une méthode de statistique exploratoire permettant de comprendre les données
Objectifs des méthodes hiérarchiques
- Mettre en évidence des relations hiérarchiques entre individus ou groupes d'individus
- Construction d'une structure arborescente représentant un emboîtement de partitions
- Chaque niveau de la hiérarchie correspond à une partition particulière des individus
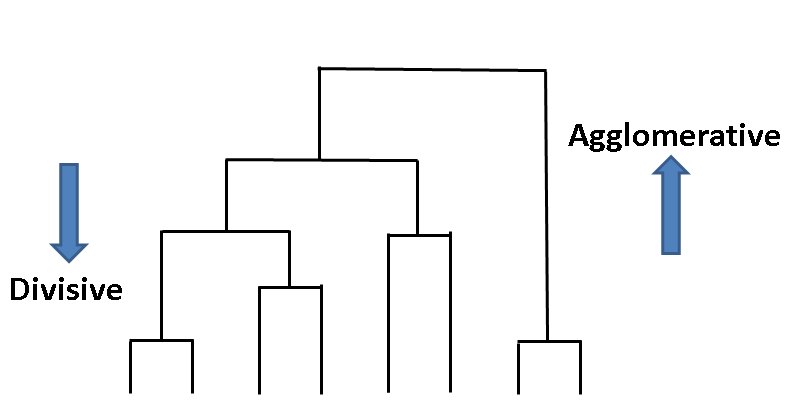
Approches possibles
Approches possibles
Une hiérarchie peut être obtenue par deux types de méthodes :
- la classification ascendante (“agglomérative”),
- la classification descendante (“divisive” en anglais)
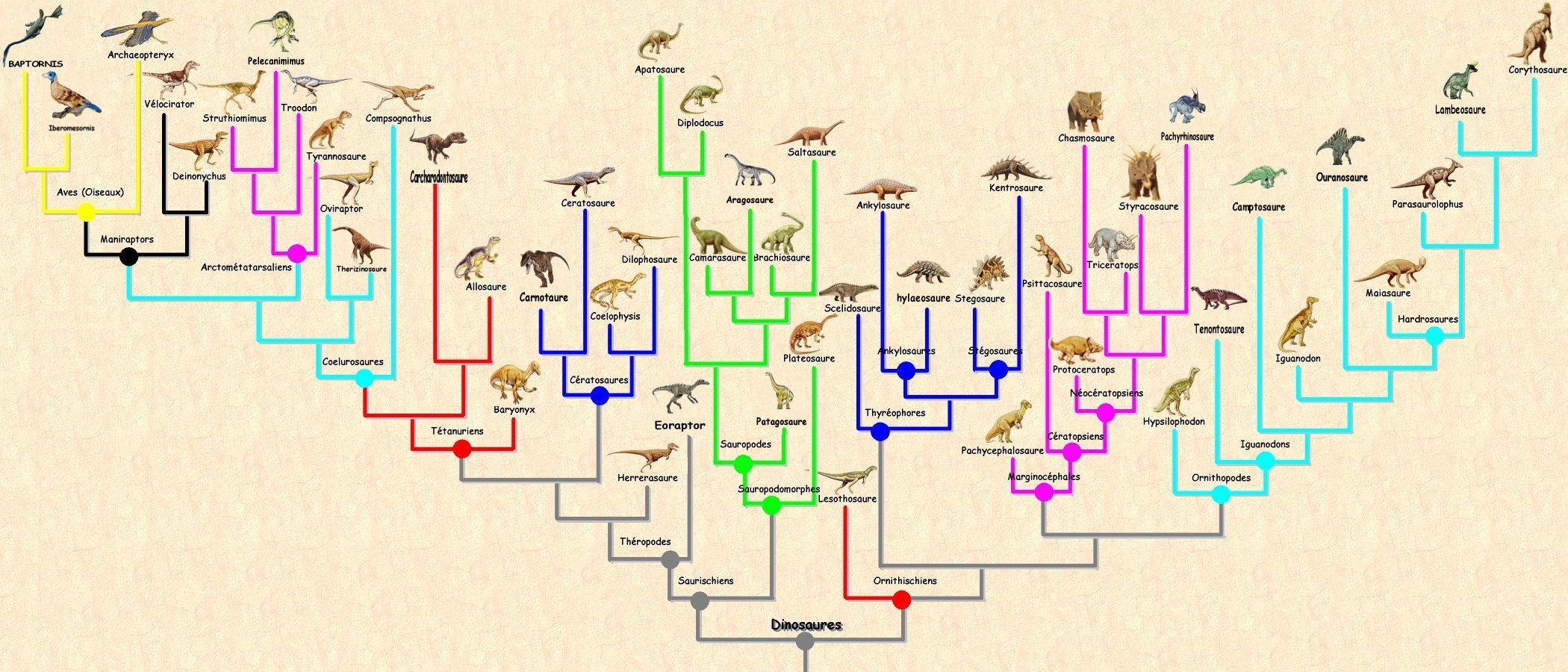
Mais au fait, qu'est ce qu'une hiérarchie ?
Notion de hiérarchie
Hiérarchie sur un ensemble d'individus
- Soit \(\boldsymbol{X}\) un tableau de données contenant \(N\) individus \(\{\boldsymbol{x}_{1}, \ldots, \boldsymbol{x}_{N}\}\).
- Une hiérarchie \(H\) est un ensembles de classes \(C_{1}, C_{2}, \ldots\), non vides et incluses dans
\(\{1, 2, \ldots, N\}\) vérifiant :
- \(\{1, 2, \ldots, N\} \in H\)
- Pour tout \(\ell \in \{1, 2, \ldots, N\}\), \(\{\ell\} \in H\), i.e. la hiérarchie contient tous les singletons d'individu
- Pour toutes classes \(C_{i}, C_{j} \in H\), alors \(C_{i} \cap C_{j} \in \{C_{i}, C_{j}, \varnothing\}\), i.e. deux classes de la hiérarchie sont soit disjointes soit contenues l'une dans l'autre
Exemples
- Considérons un jeu de données à 7 individus \(\boldsymbol{X} = \{\boldsymbol{x}_{1}, \boldsymbol{x}_{2}, \boldsymbol{x}_{3}, \boldsymbol{x}_{4}, \boldsymbol{x}_{5}, \boldsymbol{x}_{6}, \boldsymbol{x}_{7}\}\)
- L'ensemble \(H = \{\{1\}, \ldots, \{7\}, \{4,5\}, \{2,3\}, \{4,5,6\}, \{1,2,3\}, \{4,5,6,7\}, \{1, 2, 3, 4, 5, 6, 7\}\}\) est une hiérarchie sur \(\boldsymbol{X}\)
Classification Ascendante Hiérarchique
Principe général
Intuition
- On démarre en considérant une partition dans laquelle il y a autant de classes que d'individus, i.e. chaque individu est seul dans sa classe
- On regroupe alors les deux classes les plus proches (notion de proximité entre deux classes à définir !) créant ainsi une nouvelle classe plus importante
- On recommence l'opération de regroupement jusqu'à ce qu'il n'y ait plus qu'une seul classe contenant tous les individus
- Au final, nous obtenons un emboîtement de classes qui peut se mettre sous la forme d'un arbre hiérarchique appelé dendrogramme
Représentation avec un dendrogramme
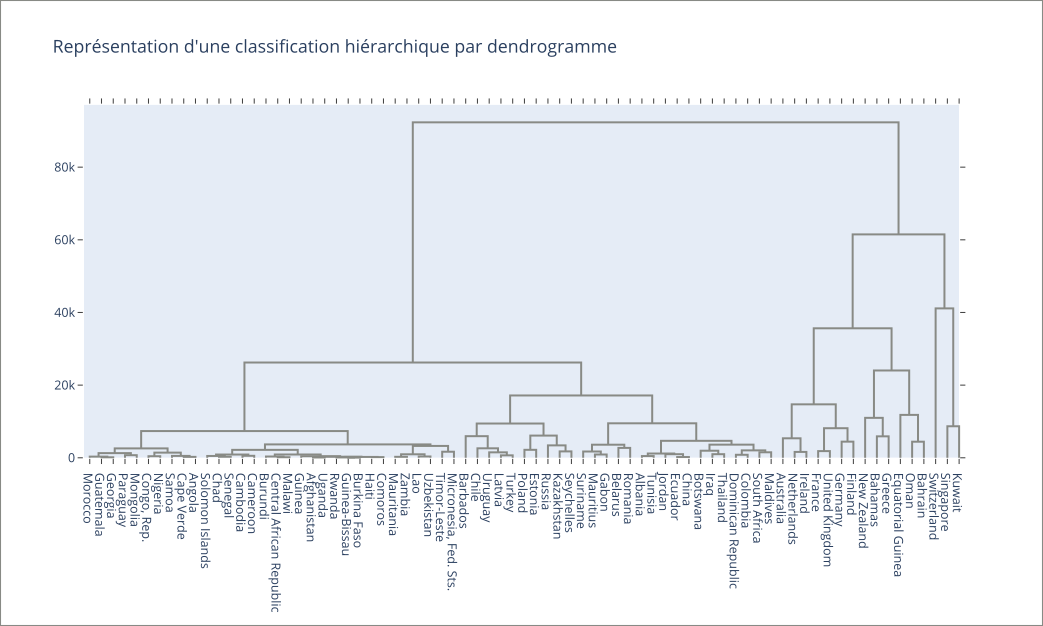
Représentation avec un dendrogramme
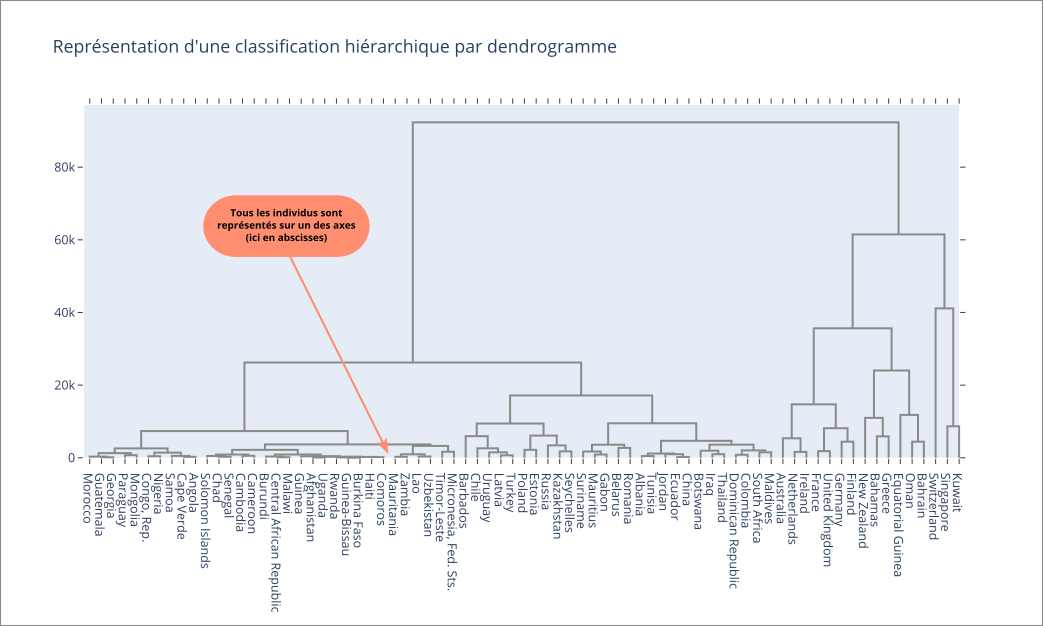
Représentation avec un dendrogramme
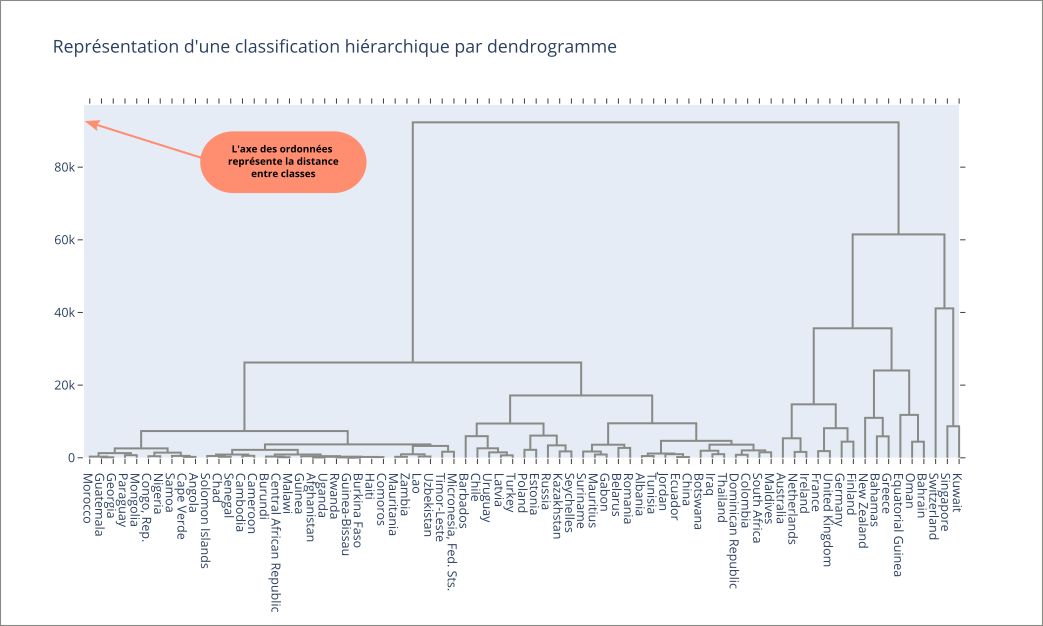
Représentation avec un dendrogramme
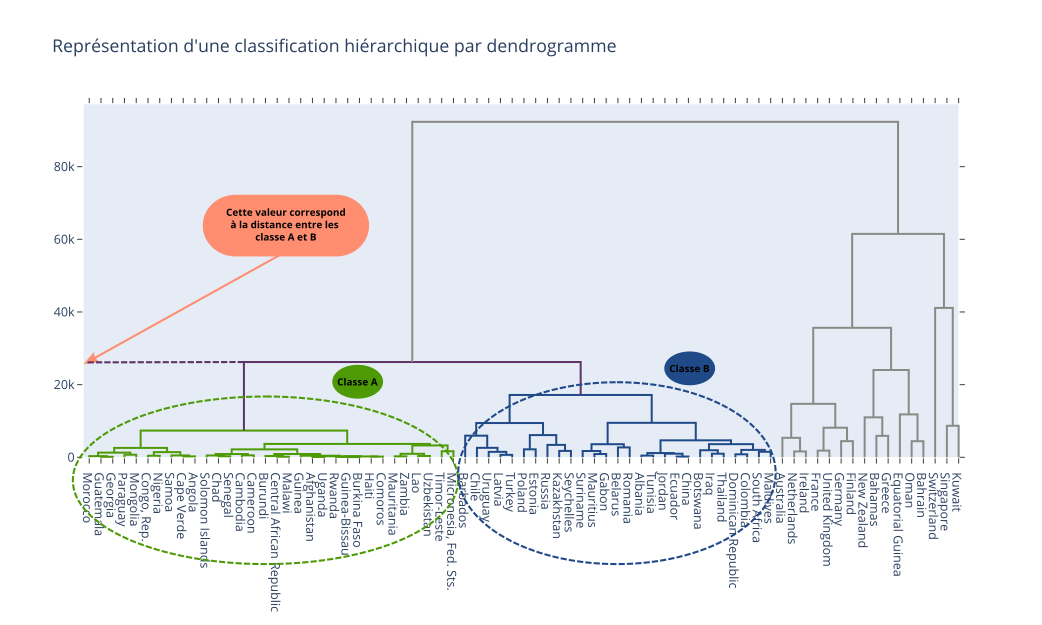
Représentation avec un dendrogramme
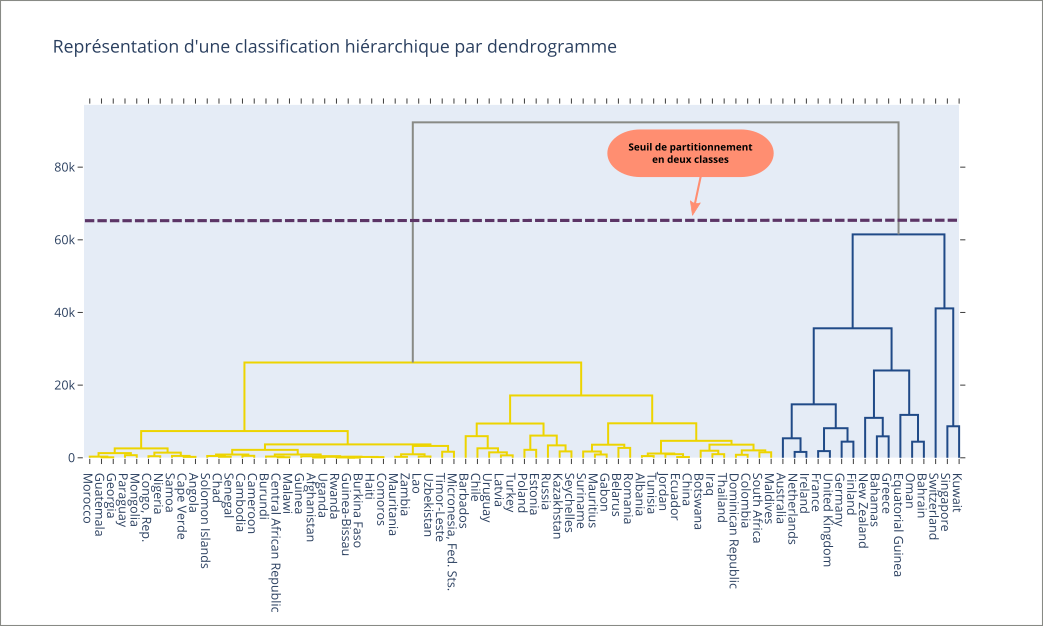
Représentation avec un dendrogramme
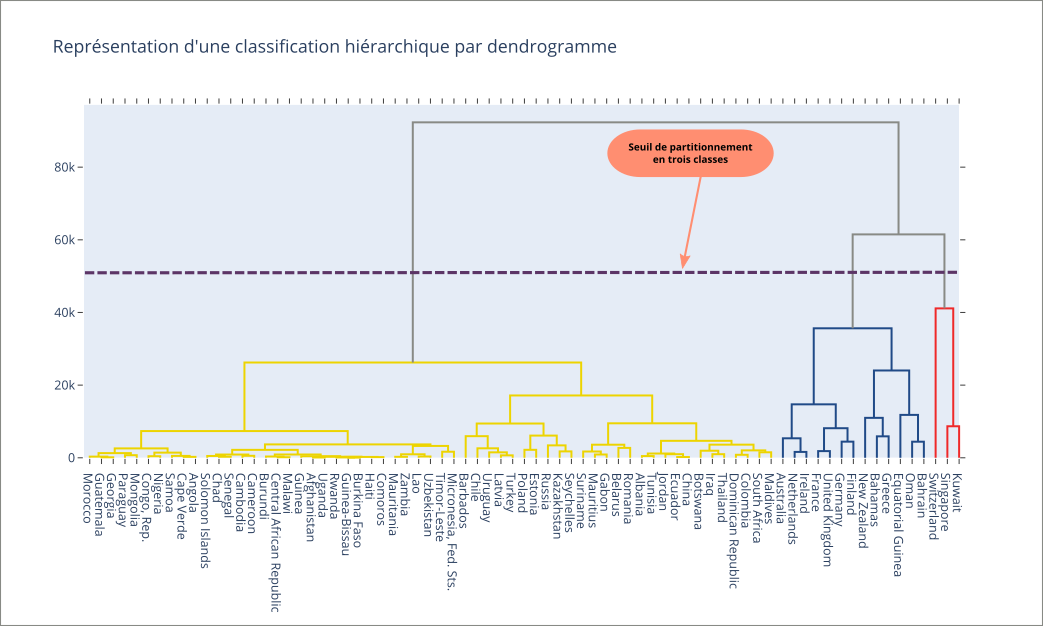
Distance entre classes
Problématique
- Nous avons déjà vu comment mesurer la proximité entre deux individus grâce à la notion de distance (ou plus généralement de dissimilarité)
- On se demande à présent comment mesurer la ressemblance entre deux groupes d'individus
Démarche
- Dans la suite de cette section, nous allons considérer :
- \(\boldsymbol{X} = \{\boldsymbol{x}_{1}, \ldots, \boldsymbol{x}_{N}\}\) : un ensemble d'individus définis sur \(\mathbb{R}^{D}\)
- Une distance \(d\) définie sur \(\mathbb{R}^{D}\) (e.g. distance euclidienne).
- Dans les sections suivantes, nous introduisons différentes "distances" entre classes, notées \(\Delta_{d}\), qui permettront de mesurer le degré de ressemblance entre deux groupes (classes) distincts \(C, C^{\prime} \subset \{1, \ldots, N\}\) d'individus
Distance entre classes
- Données avec partition :
| life_expec | total_fer | inflation | cls | |
|---|---|---|---|---|
| country | ||||
| Samoa | 71.50 | 4.34 | 1.72 | C2 |
| Iraq | 67.20 | 4.56 | 16.60 | C1 |
| Netherlands | 80.70 | 1.79 | 0.85 | C1 |
| Paraguay | 74.10 | 2.73 | 6.10 | C3 |
| Oman | 76.10 | 2.90 | 15.60 | C3 |
| Suriname | 70.30 | 2.52 | 7.20 | C3 |
| Mauritius | 73.40 | 1.57 | 1.13 | C2 |
| Central African Republic | 47.50 | 5.21 | 2.01 | C3 |
| Rwanda | 64.60 | 4.51 | 2.61 | C1 |
| Afghanistan | 56.20 | 5.82 | 9.44 | C2 |
- Calcul de la matrice des distances euclidiennes entre individus qui servira pour le calcul des distances entre classes :
| country | Samoa | Iraq | Netherlands | Paraguay | Oman | Suriname | Mauritius | Central African Republic | Rwanda | Afghanistan |
|---|---|---|---|---|---|---|---|---|---|---|
| country | ||||||||||
| Samoa | 0.00 | 15.49 | 9.59 | 5.34 | 14.69 | 5.90 | 3.41 | 24.02 | 6.96 | 17.20 |
| Iraq | 15.49 | 0.00 | 20.93 | 12.70 | 9.11 | 10.11 | 16.93 | 24.52 | 14.23 | 13.19 |
| Netherlands | 9.59 | 20.93 | 0.00 | 8.49 | 15.49 | 12.21 | 7.31 | 33.40 | 16.42 | 26.27 |
| Paraguay | 5.34 | 12.70 | 8.49 | 0.00 | 9.71 | 3.96 | 5.15 | 27.03 | 10.28 | 18.47 |
| Oman | 14.69 | 9.11 | 15.49 | 9.71 | 0.00 | 10.21 | 14.78 | 31.75 | 17.42 | 21.04 |
| Suriname | 5.90 | 10.11 | 12.21 | 3.96 | 10.21 | 0.00 | 6.88 | 23.54 | 7.58 | 14.65 |
| Mauritius | 3.41 | 16.93 | 7.31 | 5.15 | 14.78 | 6.88 | 0.00 | 26.17 | 9.40 | 19.57 |
| Central African Republic | 24.02 | 24.52 | 33.40 | 27.03 | 31.75 | 23.54 | 26.17 | 0.00 | 17.12 | 11.46 |
| Rwanda | 6.96 | 14.23 | 16.42 | 10.28 | 17.42 | 7.58 | 9.40 | 17.12 | 0.00 | 10.91 |
| Afghanistan | 17.20 | 13.19 | 26.27 | 18.47 | 21.04 | 14.65 | 19.57 | 11.46 | 10.91 | 0.00 |
Distance entre classes
Lien minimum
La distance du lien minimum (single link en anglais) entre \(C\) et \(C^{\prime}\) est définie par : \[ \Delta_{d}(C, C^{\prime}) = \underset{\ell \in C,~ m \in C^{\prime}}{\min} d(\boldsymbol{x}_{\ell},\boldsymbol{x}_{m}) \]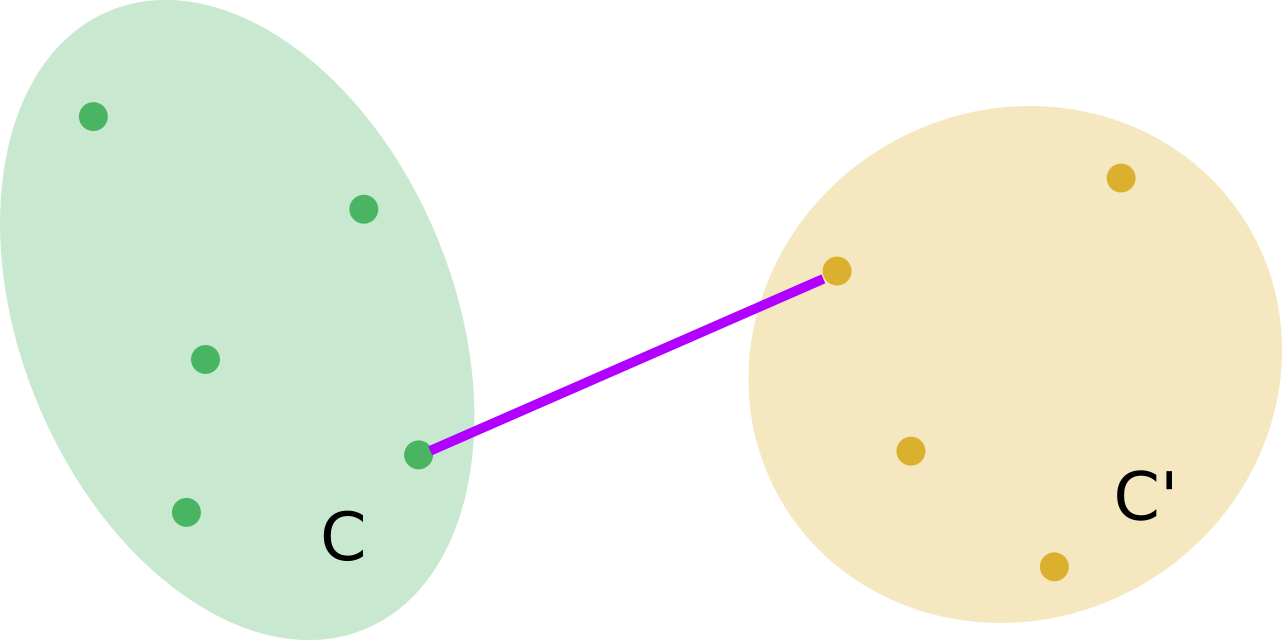
Exemple
- Distances entre les individus des classes \(C_{1}\) et \(C_{2}\) :
| country | Samoa | Mauritius | Afghanistan |
|---|---|---|---|
| country | |||
| Iraq | 15.49 | 16.93 | 13.19 |
| Netherlands | 9.59 | 7.31 | 26.27 |
| Rwanda | 6.96 | 9.40 | 10.91 |
- \(\Delta_{d}(C_{1}, C_{2}) \simeq\) 6.96
Distance entre classes
Lien maximum
La distance du lien maximum (complete link en anglais) entre \(C\) et \(C^{\prime}\) est définie par : \[ \Delta_{d}(C, C^{\prime}) = \underset{\ell \in C,~ m \in C^{\prime}}{\max} d(\boldsymbol{x}_{\ell},\boldsymbol{x}_{m}) \]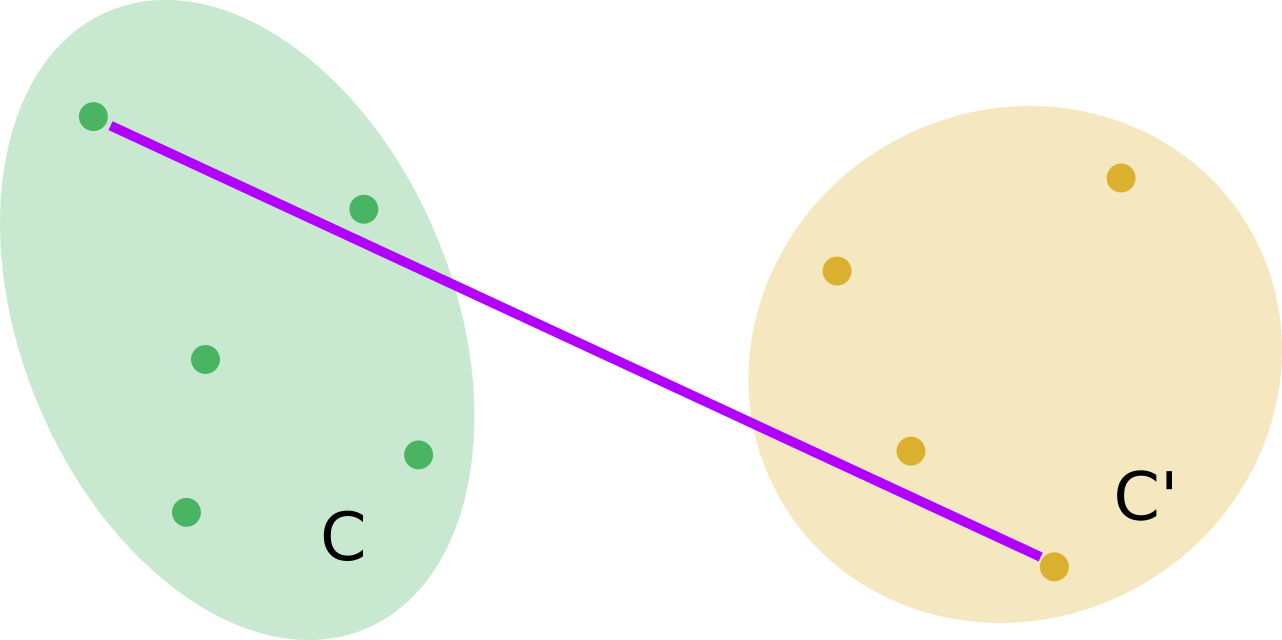
Exemple
- Distances entre les individus des classes \(C_{1}\) et \(C_{3}\) :
| country | Paraguay | Oman | Suriname | Central African Republic |
|---|---|---|---|---|
| country | ||||
| Iraq | 12.70 | 9.11 | 10.11 | 24.52 |
| Netherlands | 8.49 | 15.49 | 12.21 | 33.40 |
| Rwanda | 10.28 | 17.42 | 7.58 | 17.12 |
- \(\Delta_{d}(C_{1}, C_{3}) \simeq\) 33.40
Distance entre classes
Distance moyenne
La distance moyenne (group average en anglais) entre \(C\) et \(C^{\prime}\) est définie par : \[ \Delta_{d}(C, C^{\prime}) = \frac{1}{N_{C} \cdot N_{C^{\prime}}} \sum_{\ell \in C} \sum_{m \in C^{\prime}} d(\boldsymbol{x}_{\ell},\boldsymbol{x}_{m}) \] avec \(N_{C} = \text{Card}(C)\) et \(N_{C^{\prime}} = \text{Card}(C^{\prime})\)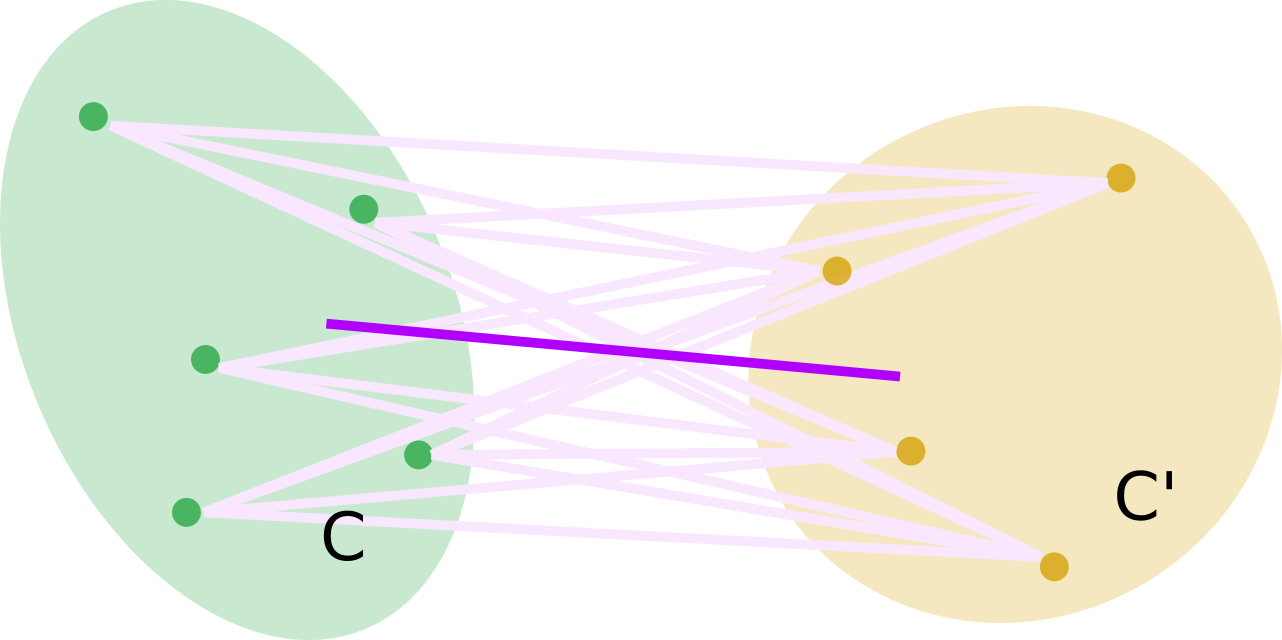
Exemple
- Distances entre les individus des classes \(C_{2}\) et \(C_{3}\) :
| country | Paraguay | Oman | Suriname | Central African Republic |
|---|---|---|---|---|
| country | ||||
| Samoa | 5.34 | 14.69 | 5.90 | 24.02 |
| Mauritius | 5.15 | 14.78 | 6.88 | 26.17 |
| Afghanistan | 18.47 | 21.04 | 14.65 | 11.46 |
- \(\Delta_{d}(C_{2}, C_{3}) \simeq\) 14.05
Distance entre classes
Distance de Ward
- La distance de Ward entre \(C\) et \(C^{\prime}\) est définie par :
\[
\Delta_{\text{ward}}(C, C^{\prime}) = \frac{N_{C} \cdot N_{C^{\prime}}}{N_{C} + N_{C^{\prime}}}
d(\boldsymbol{\mu}_{C}, \boldsymbol{\mu}_{C^{\prime}})^{2}
\]
- \(N_{C} = \text{Card}(C)\) et \(N_{C^{\prime}} = \text{Card}(C^{\prime})\)
- \(\boldsymbol{\mu}_{C}, \boldsymbol{\mu}_{C^{\prime}}\), les centres de gravité des classe \(C\) et \(C^{\prime}\)
- Cette distance correspond à la distance euclidienne entre les barycentres au carré des deux classes, pondérée par leur effectif
Exemple
- Centres de gravité de chaque classe :
| life_expec | total_fer | inflation | |
|---|---|---|---|
| cls | |||
| C1 | 70.83 | 3.62 | 6.69 |
| C2 | 67.03 | 3.91 | 4.10 |
| C3 | 67.00 | 3.34 | 7.73 |
- \(\Delta_{\text{ward}}(C_{1}, C_{2}) \simeq\) 31.84
- \(\Delta_{\text{ward}}(C_{1}, C_{3}) \simeq\) 27.18
- \(\Delta_{\text{ward}}(C_{2}, C_{3}) \simeq\) 23.16
Distance entre classes
Propriété
- Soient \(\boldsymbol{X}\) un tableau de données contenant \(N\) individus et \(C, C^{\prime} \subset \{1, \ldots, N\}\) deux groupes (classes) distincts d'individus
- Nous avons alors la relation suivante : \[ I_{\boldsymbol{\mu}_{C \cup C^{\prime}}}(C \cup C^{\prime}) = I_{\boldsymbol{\mu}_{C}}(C) + I_{\boldsymbol{\mu}_{C^{\prime}}}(C^{\prime}) + \Delta_{\text{ward}}(C, C^{\prime}) \]
Interprétation
- La distance de Ward représente l'augmentation de l'inertie intra-classe induite par le regroupement (la fusion) de deux classes au sein d'une partition donnée
- Utiliser la distance de Ward pour regrouper les classes permet donc d'assurer que l'augmentation de l'inertie intra-classe soit minimum (ou de manière équivalente que l'augmentation de l'inertie inter-classe soit maximum) à chaque regroupement
Exemple : déroulement d'une CAH
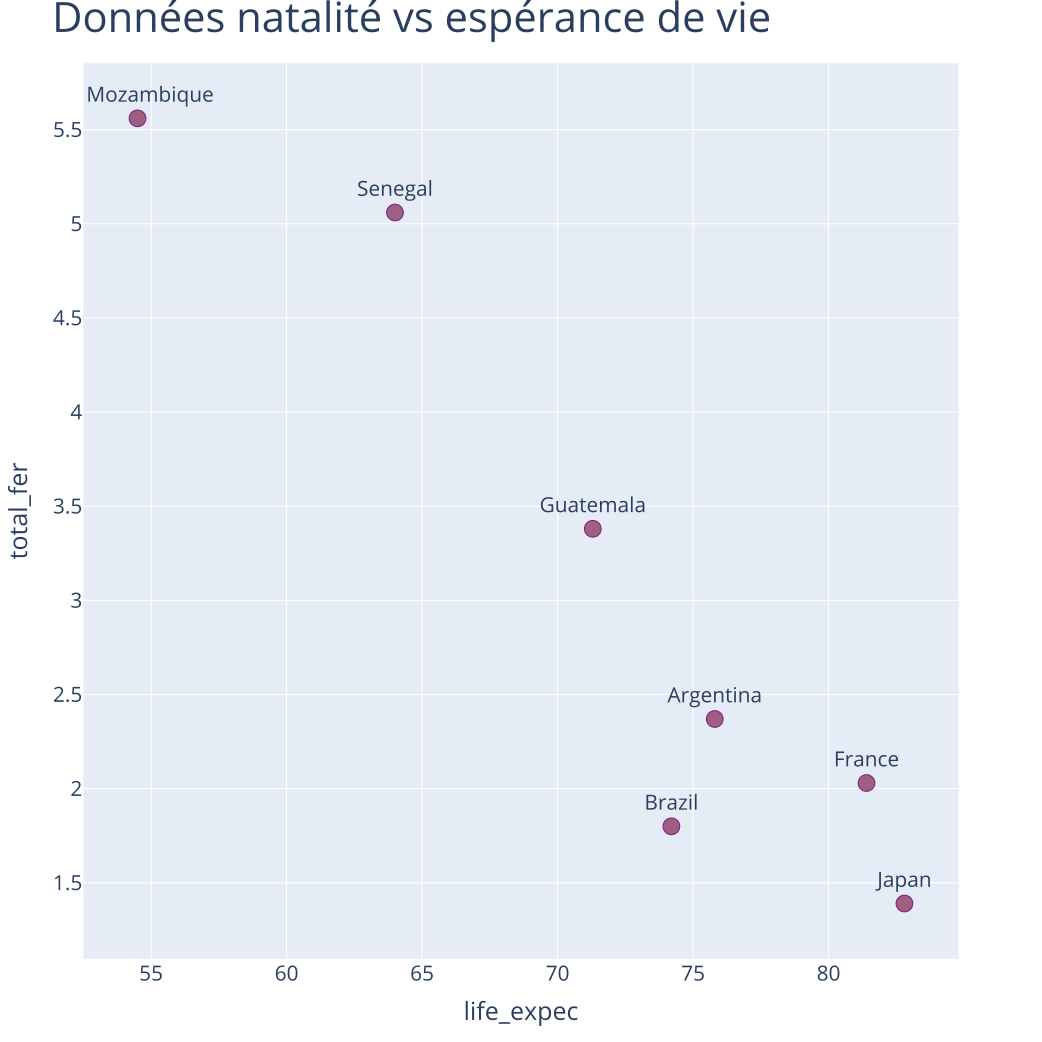
Données :
| life_expec | total_fer | |
|---|---|---|
| country | ||
| France | 81.40 | 2.03 |
| Mozambique | 54.50 | 5.56 |
| Guatemala | 71.30 | 3.38 |
| Brazil | 74.20 | 1.80 |
| Japan | 82.80 | 1.39 |
| Argentina | 75.80 | 2.37 |
| Senegal | 64.00 | 5.06 |
Exemple : CAH - Initialisation
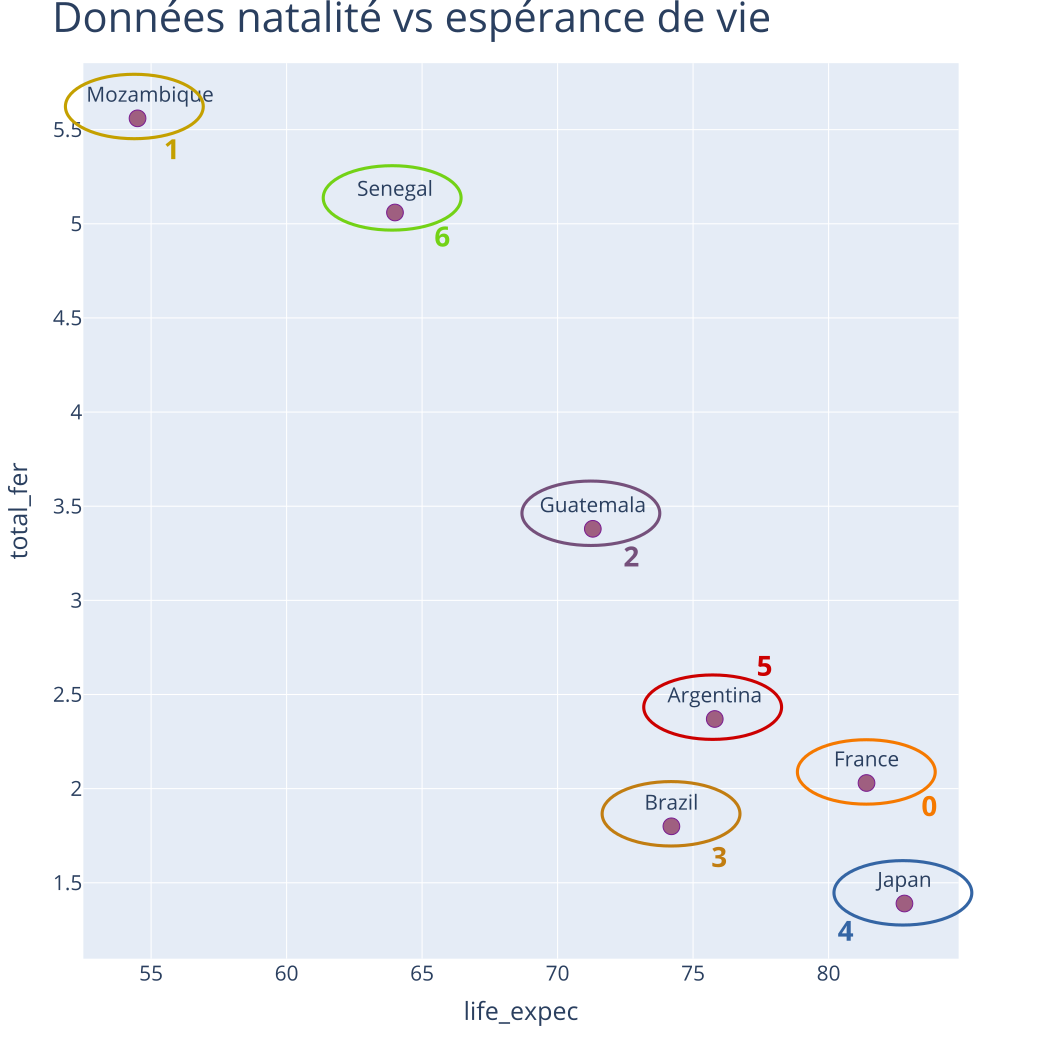
Partition initiale à \(K = 7\) classes
Distances entre classes (Ward) :
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|---|
| 0 | 368.04 | 51.92 | 25.95 | 1.18 | 15.74 | 155.97 | |
| 1 | 143.50 | 201.11 | 409.14 | 231.93 | 45.25 | ||
| 2 | 5.45 | 68.11 | 10.64 | 28.06 | |||
| 3 | 37.06 | 1.44 | 57.33 | ||||
| 4 | 24.98 | 183.45 | |||||
| 5 | 73.24 | ||||||
| 6 |
Exemple : CAH - Itération 1
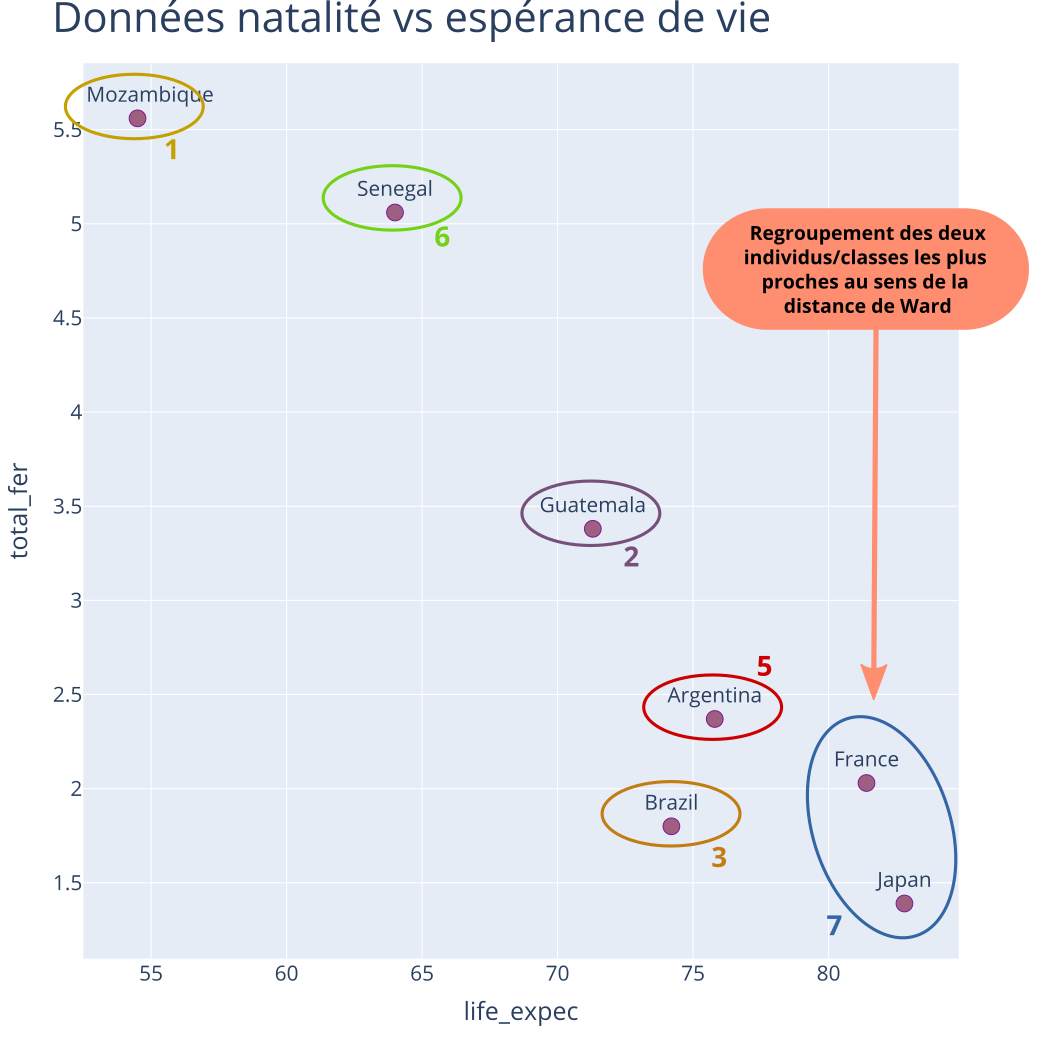
Partition à \(K = 6\) classes
Distances entre classes (Ward) :
| 1 | 2 | 3 | 5 | 6 | 7 | |
|---|---|---|---|---|---|---|
| 1 | 143.50 | 201.11 | 231.93 | 45.25 | 517.72 | |
| 2 | 5.45 | 10.64 | 28.06 | 79.62 | ||
| 3 | 1.44 | 57.33 | 41.61 | |||
| 5 | 73.24 | 26.75 | ||||
| 6 | 225.89 | |||||
| 7 |
Exemple : CAH - Itération 2
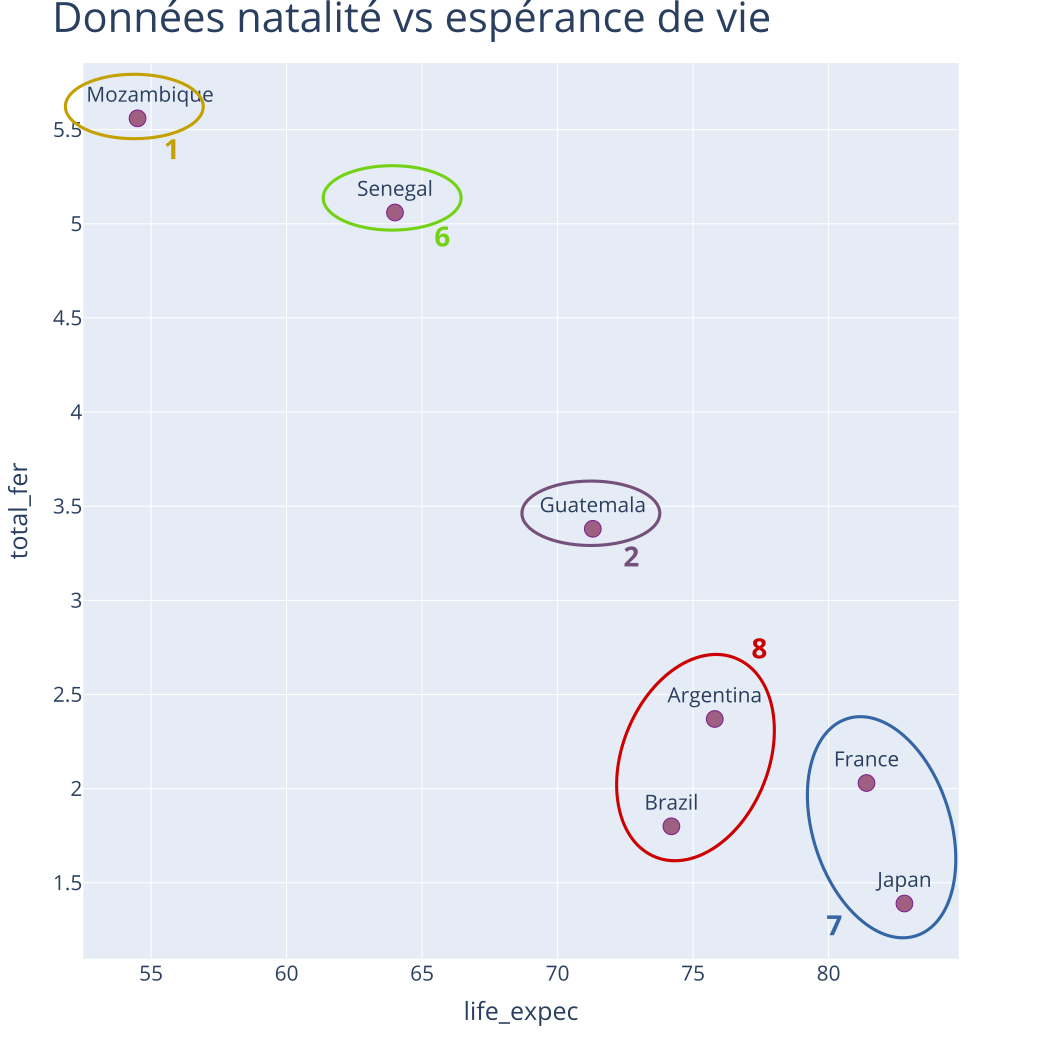
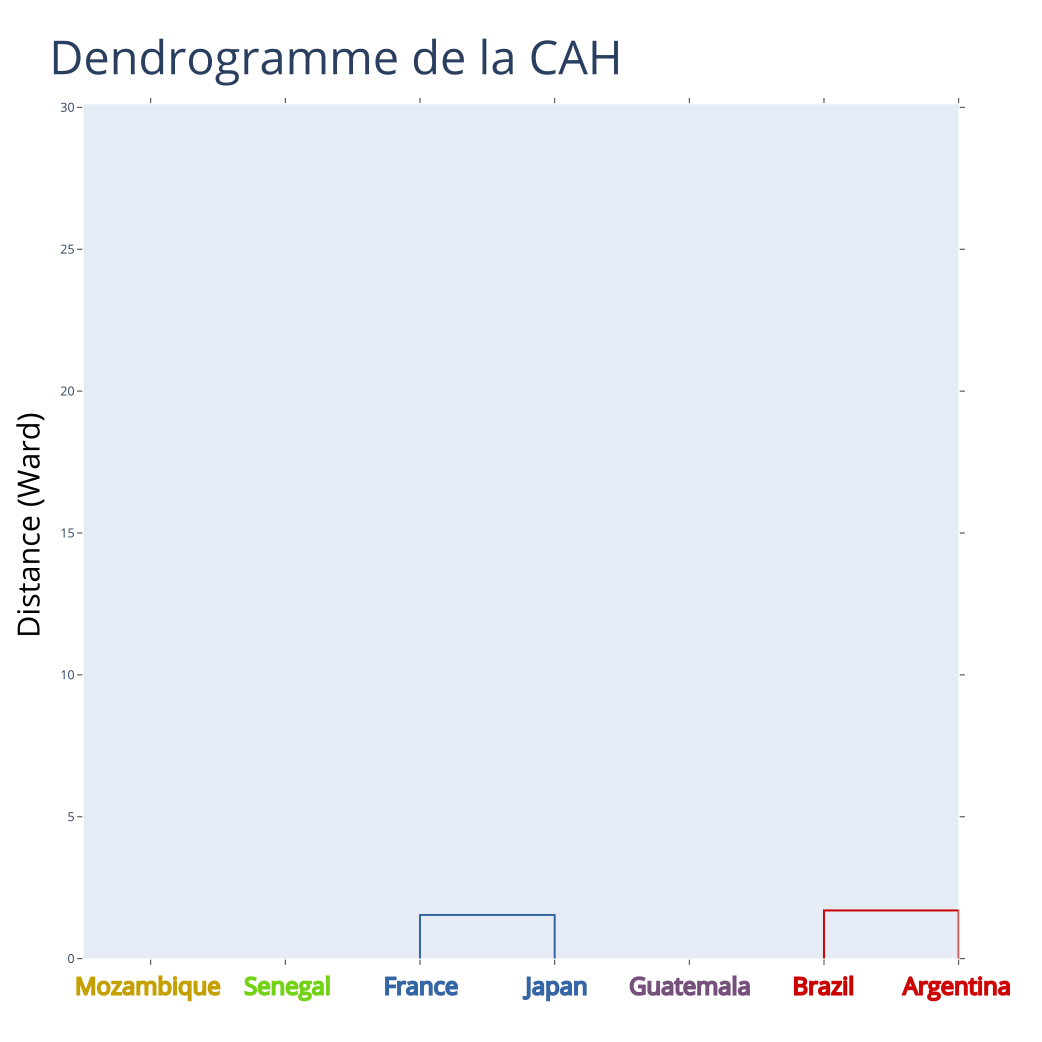
Partition à \(K = 5\) classes
Distances entre classes (Ward) :
| 1 | 2 | 6 | 7 | 8 | |
|---|---|---|---|---|---|
| 1 | 143.50 | 45.25 | 517.72 | 288.22 | |
| 2 | 28.06 | 79.62 | 10.24 | ||
| 6 | 225.89 | 86.57 | |||
| 7 | 50.55 | ||||
| 8 |
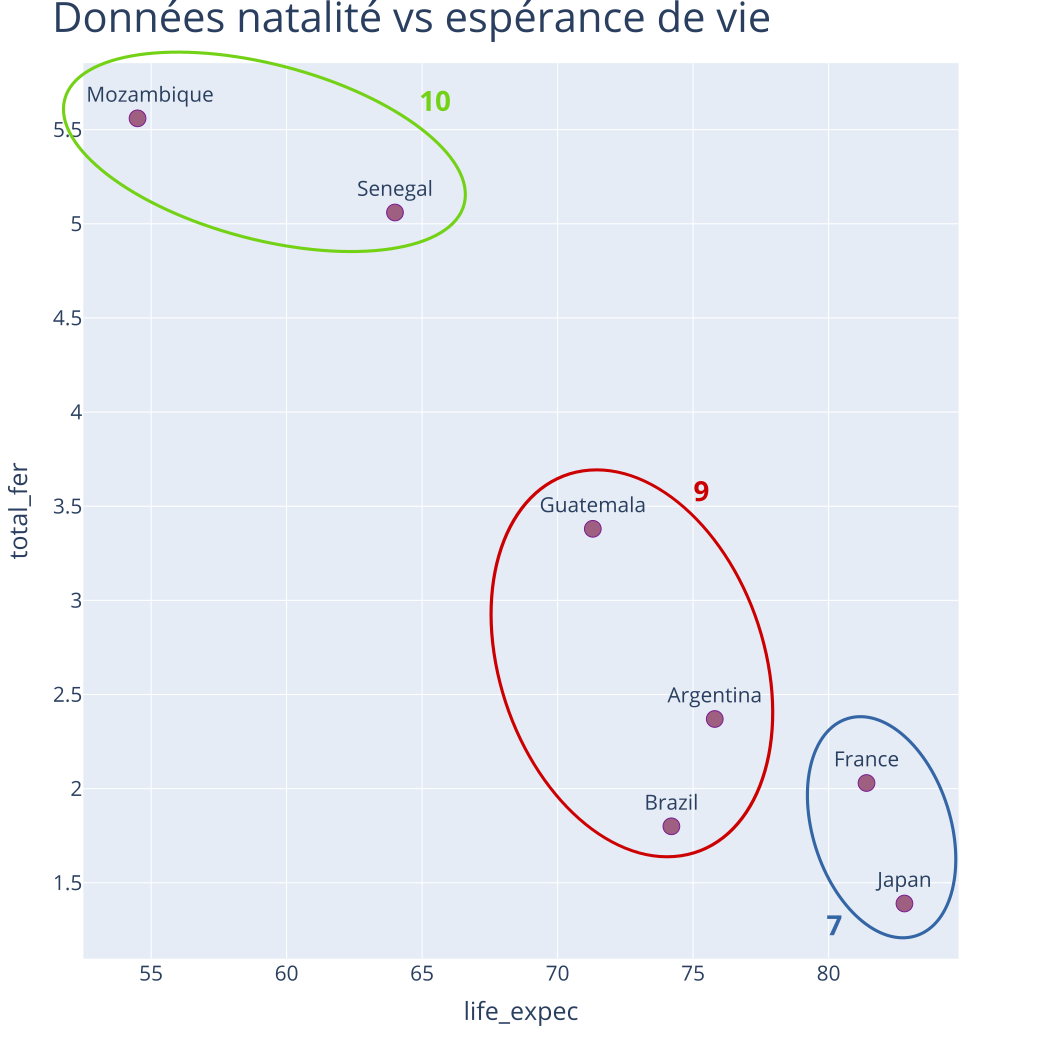
Exemple : CAH - Itération 3
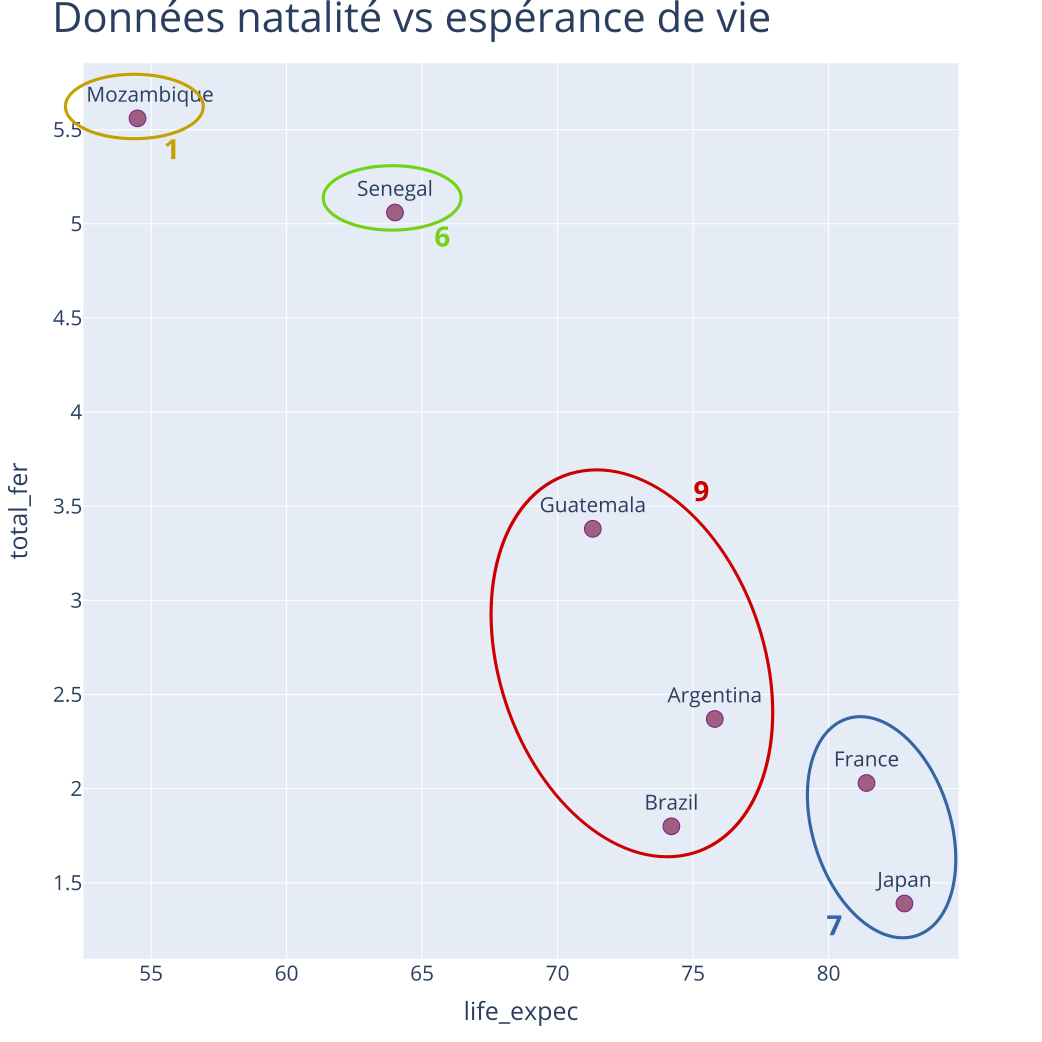
Partition à \(K = 4\) classes
Distances entre classes (Ward) :
| 1 | 6 | 7 | 9 | |
|---|---|---|---|---|
| 1 | 45.25 | 517.72 | 285.35 | |
| 6 | 225.89 | 76.39 | ||
| 7 | 84.11 | |||
| 9 |
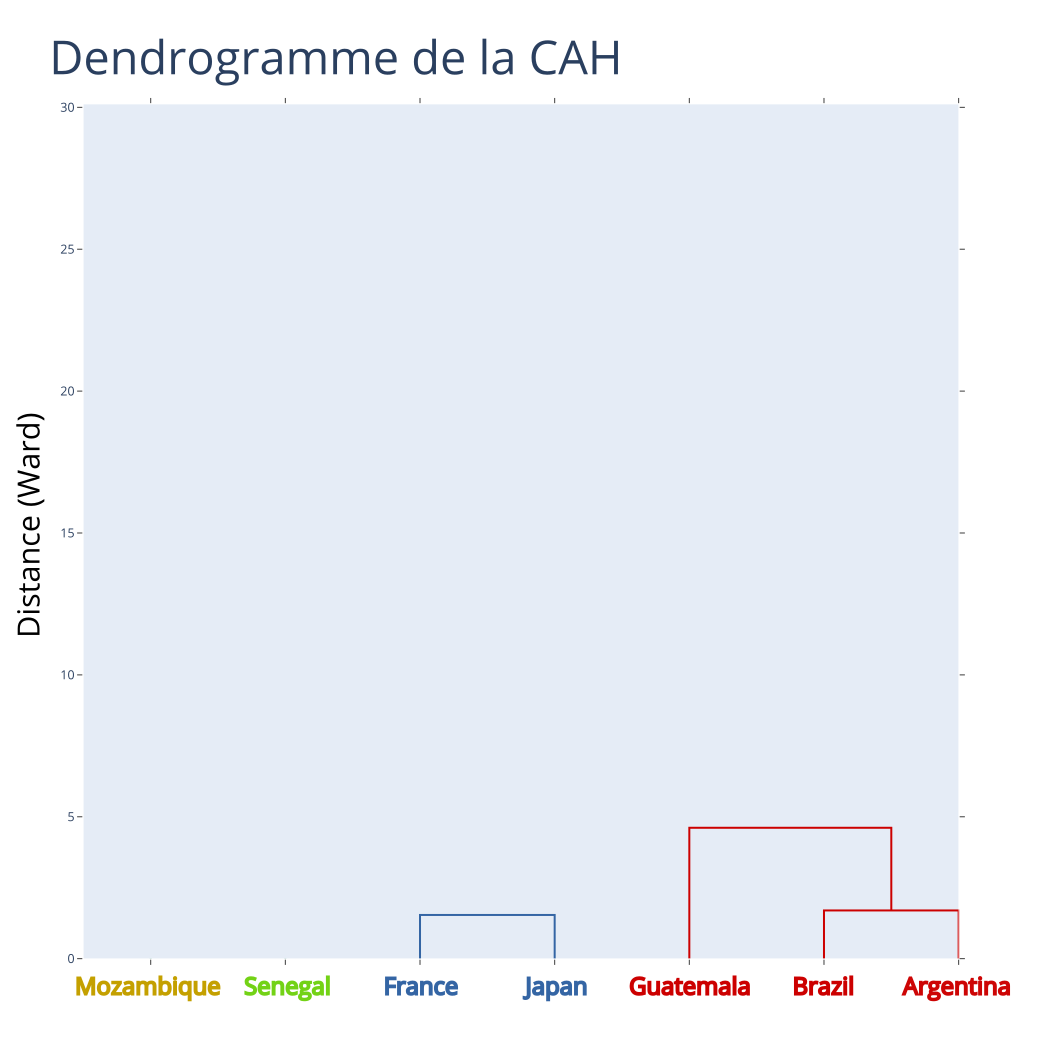
Exemple : CAH - Itération 4
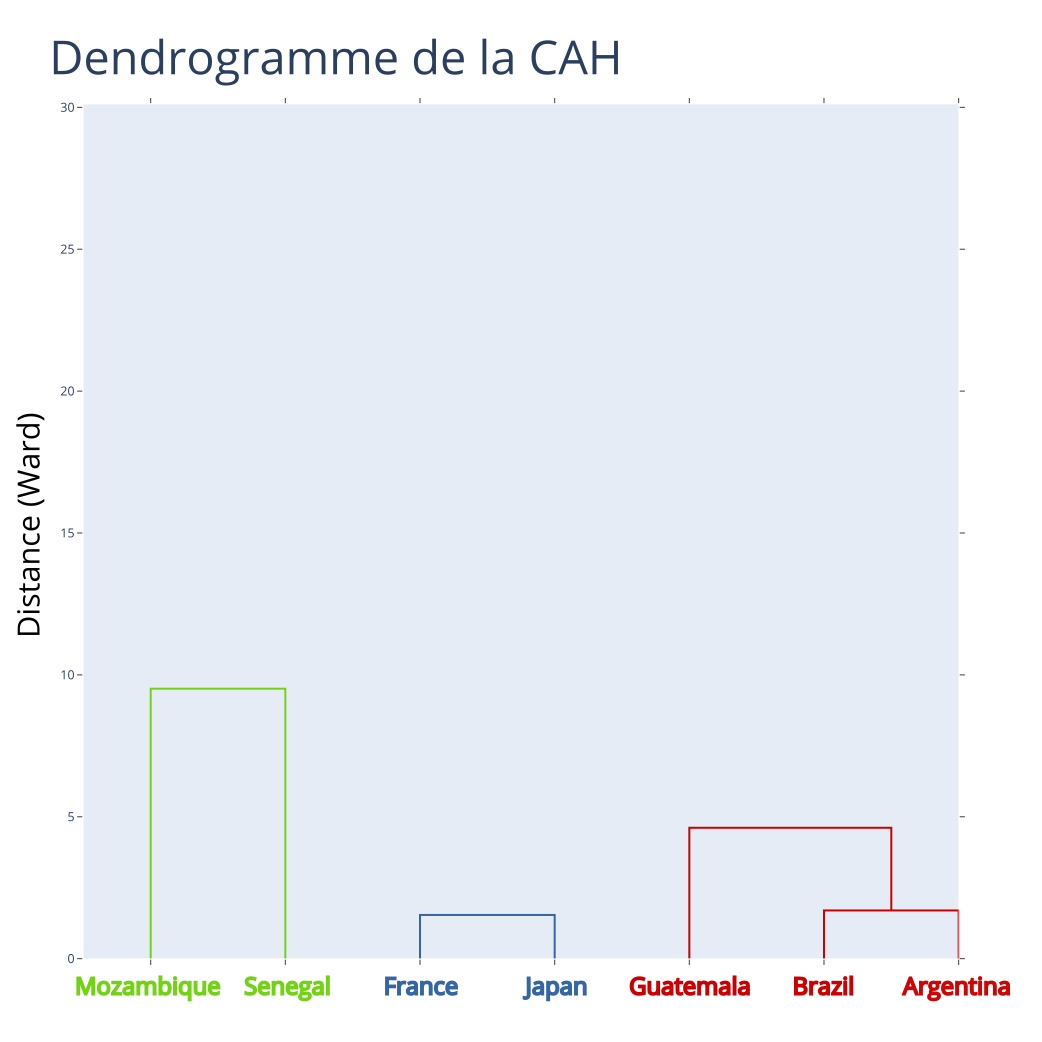
Partition à \(K = 3\) classes
Distances entre classes (Ward) :
| 7 | 9 | 10 | |
|---|---|---|---|
| 7 | 84.11 | 535.08 | |
| 9 | 262.24 | ||
| 10 |
Exemple : CAH - Itération 5
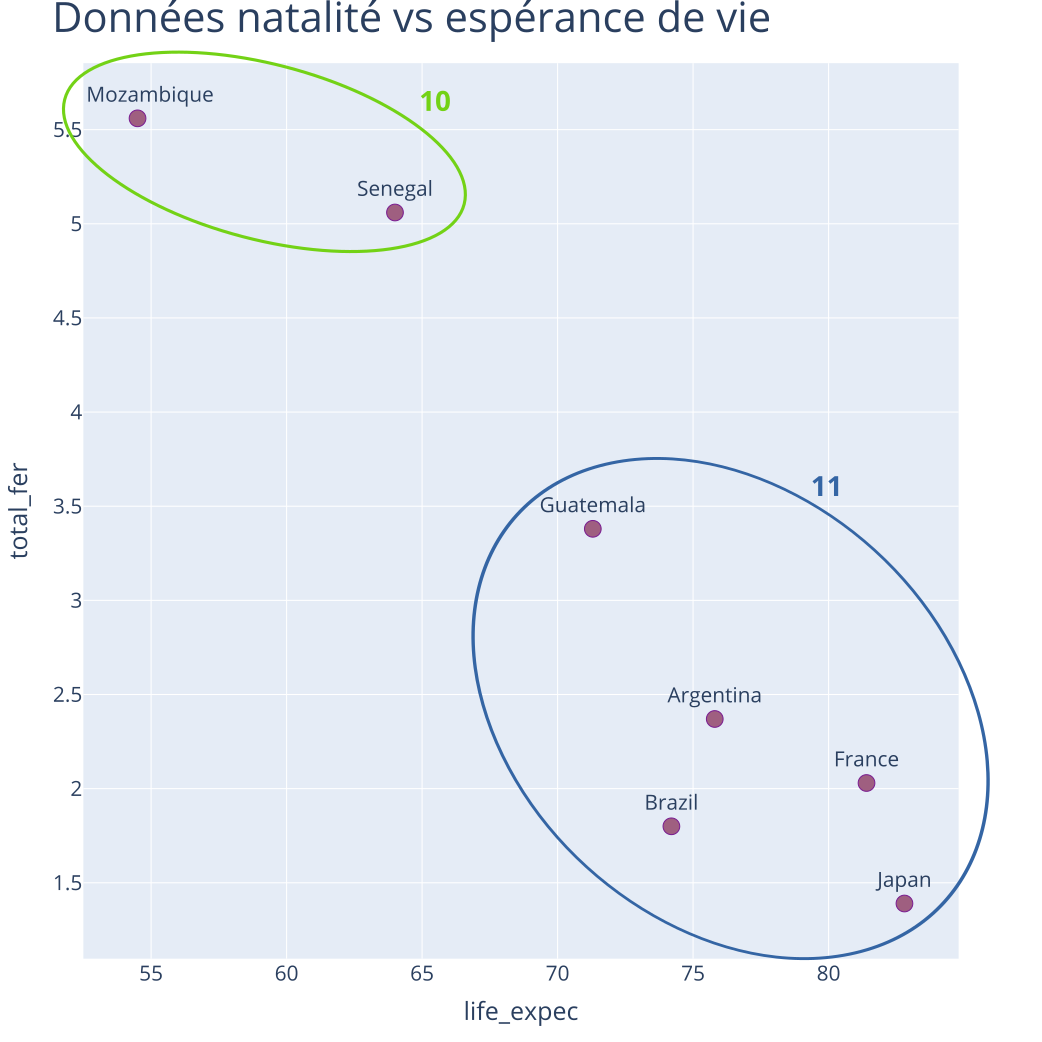
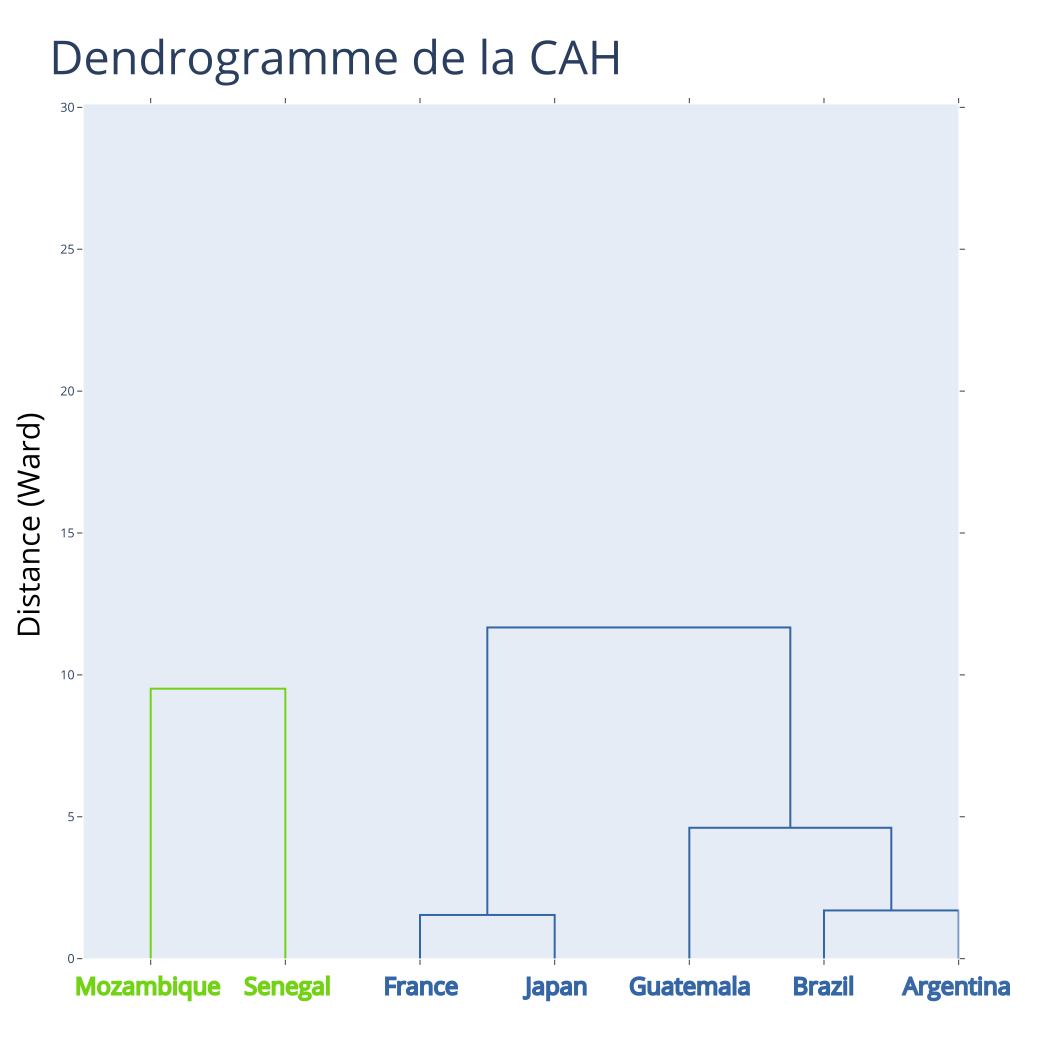
Partition à \(K = 2\) classes
Distances entre classes (Ward) :
| 10 | 11 | |
|---|---|---|
| 10 | 469.05 | |
| 11 |
Exemple : CAH - Fin
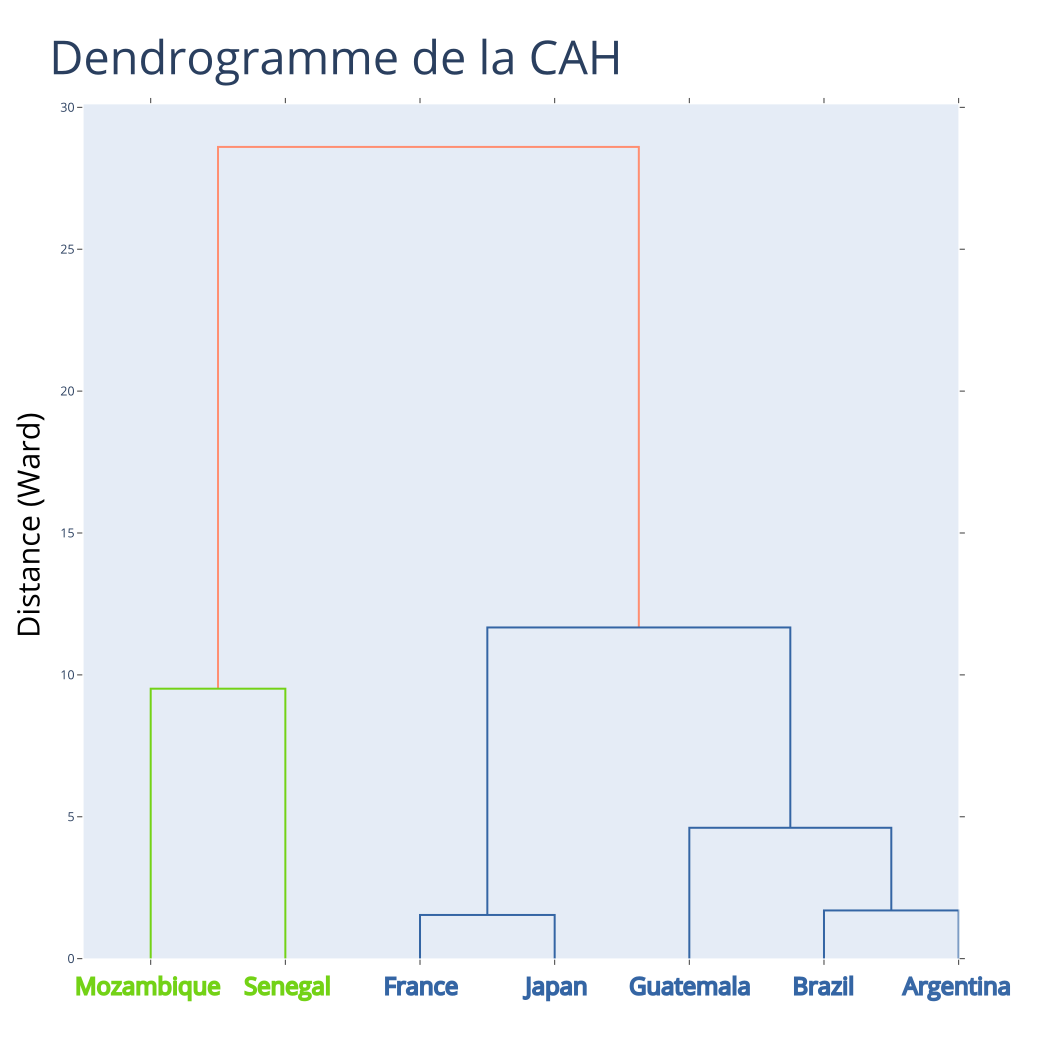
- L'algorithme a regroupé tous les individus en deux classes
- Il suffit d'ajouter la partition trivial à une classe contenant tous les individus pour achever la hiérarchie
- Calcul du nombre de classes pertinent par expertise et en utilisant la méthode du "coude"
Algorithme formel
Entrées/Sorties
- Entrée : \(\boldsymbol{X} = \{\boldsymbol{x}_{1}, \ldots, \boldsymbol{x}_{N}\}\) un ensemble d'individus dans \(\mathbb{R}^{D}\)
- Paramètres :
- \(\Delta_{d}\) : Une distance entre deux classes, appelée distance d'agrégation, reposant sur la distance entre individus notée \(d\)
- Sortie : Une hiérarchie \(H\) sur les individus \(\boldsymbol{X}\)
Initialisation
- On part de la partition des singletons à \(N\) classes \(C^{(0)} = \{C^{(0)}_{1}, \ldots, C^{(0)}_{N}\}\) où pour tout \(n\), la classe \(C^{(0)}_{n} = \{n\}\)
- On initialise la hiérarchie \(H^{(0)}\) avec cette première partition, i.e. \(H^{(0)} \leftarrow \{C^{(0)}\}\)
Algorithme formel
Itérations
- Calculer la distance d'agrégation entre chaque paire de classes de la partition \(C^{(t-1)}\) afin de trouver les deux classes les plus proches, notées \(C^{(t-1)}_{\ell^{*}}\) et \(C^{(t-1)}_{m^{*}}\) : \[ C^{(t-1)}_{\ell^{*}}, C^{(t-1)}_{m^{*}} = \underset{C^{(t-1)}_{\ell}, C^{(t-1)}_{m} \in C^{(t-1)}}{\operatorname{arg min}} \Delta_{d}(C^{(t-1)}_{\ell}, C^{(t-1)}_{m}) \]
- Regrouper les deux classes les plus proches : \[ C^{(t)}_{*} \leftarrow C^{(t-1)}_{\ell^{*}} \cup C^{(t-1)}_{m^{*}} \]
- Mettre à jour la partition courante en ajoutant la classe formée du regroupement des deux classes les plus proches et en supprimant ces deux classes individuellement : \[ C^{(t)} \leftarrow C^{(t-1)} \cup C^{(t)}_{*} \setminus \{C^{(t-1)}_{\ell^{*}}, C^{(t-1)}_{m^{*}}\} \]
- Mise à jour de la hiérarchie courante avec la classe formée du regroupement des deux classes les plus proches : \[ H^{(t)} \leftarrow H^{(t - 1)} \cup C^{(t)}_{*} \]
- Continuer tant que la partition courante \(C^{(t)}\) contient au moins deux classes
Influence de la distance d'agrégation
Influence de la distance d'agrégation
Influence de la distance d'agrégation
Influence de la distance d'agrégation
Forces et Faiblesses
Forces
- Méthode "facile" à comprendre et à implémenter
- L'algorithme fonctionne sans a priori sur le nombre de classes
- La méthode converge toujours vers la même hiérarchie (en fixant la distance d'agrégation)
- Visualisation efficace sous forme de dendrogramme quand le nombre de données n'est pas trop grand
Faiblesses
- La méthode dépend fortement du choix de la distance d'agrégation choisie (même si la distance de Ward est recommandée)
- La hiérarchie ne peut être modifiée au cours des itérations
- La méthode n'optimise pas de critère particulier
- Lorsque le nombre d'individus est grand, le dendrogramme est difficile à lire
- Complexité calculatoire fortement dépendante du nombre de données
Résumé de la séance
Points clés
- Découverte de la notion de classification hiérarchique
- Introduction au concept de distance entre classes
- Étude de l'algorithme CAH et de ses principales caractéristiques
- Interprétation et construction pratique d'un dendrogramme
Merci pour votre attention !
